
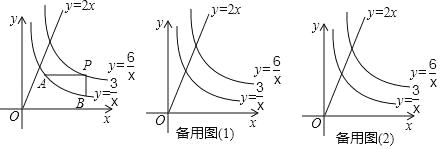
����Ŀ����֪��P��m��n���Ƿ���������y��![]() ��x��0����ͼ���ϵ�һ���㣬PA��x�ᣬPB��y�ᣬ�ֱ���������y��
��x��0����ͼ���ϵ�һ���㣬PA��x�ᣬPB��y�ᣬ�ֱ���������y��![]() ��x��0����ͼ���ڵ�A��B����C��ֱ��y��2x�ϵ�һ�㣮
��x��0����ͼ���ڵ�A��B����C��ֱ��y��2x�ϵ�һ�㣮
��1����A������Ϊ���� ������ ��������B������Ϊ���� ������ ���������ú�m�Ĵ���ʽ��ʾ��
��2���ڵ�P�˶��Ĺ����У�����AB��֤������PAB�������һ����ֵ������������ֵ��
��3���ڵ�P�˶��Ĺ����У��Ե�P��A��B��CΪ������ı����ܷ�Ϊƽ���ı��Σ����ܣ������ʱm��ֵ�������ܣ���˵�����ɣ�
���𰸡���1��![]() ����2��
����2��![]() ����3��m��3��1��
����3��m��3��1��![]()
��������
(1)����P(m��n)���뷴��������y=![]() (x��0)����m��ʾ��n���ɱ�ʾ����P�����꣬Ȼ�����PA��x�ᣬ�õ�A���������Ϊ
(x��0)����m��ʾ��n���ɱ�ʾ����P�����꣬Ȼ�����PA��x�ᣬ�õ�A���������Ϊ![]() ��Ȼ��A����������˷����������Ľ���ʽy=
��Ȼ��A����������˷����������Ľ���ʽy=![]() (x��0)���ɵõ���A�����꣬ͬ���õ���B�����ꣻ
(x��0)���ɵõ���A�����꣬ͬ���õ���B�����ꣻ
(2)����PA=m-![]() ��PB=
��PB=![]()
![]() =
=![]() ������S��PAB=
������S��PAB=![]() PAPB���ɵõ��𰸣�
PAPB���ɵõ��𰸣�
(3)����������ֱ�ͼ�Σ����ƽ���ıߵ����ʽ������ۼ���.
(1)�ߵ�P(m��n)�Ƿ���������y��![]() (x��0)ͼ���ϵĶ��㣬
(x��0)ͼ���ϵĶ��㣬
��n��![]() ��
��
���P(m��![]() )��
)��
��PA��x�ᣬ
��A���������Ϊ![]() ��
��
����A����������뷴���������Ľ���ʽy��![]() (x��0)�ã�x��
(x��0)�ã�x��![]() ��
��
��A(![]() ��
��![]() )��ͬ���ɵã�B(m��
)��ͬ���ɵã�B(m��![]() )��
)��
(2)��PA��m��![]() ��
��![]() ��PB��
��PB��![]() ��
��![]() ��
��![]() ��
��
��S��PAB��![]() PAPB��
PAPB��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
(3)�����ı���PBACΪƽ���ı��Σ�����AC��y�ᣬ
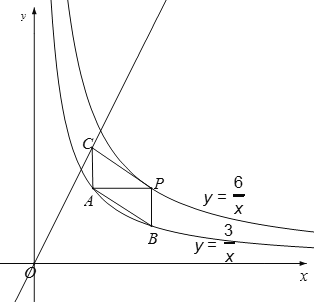
��C�������Ϊ![]() ��
��
����y��2x��C(![]() ��m)��
��m)��
��ʱAC��m��![]() ��PB��
��PB��![]() ��
��
��AC��PB���ã�m��![]() ��
��![]() ��
��
��ã�m��3��m����3(��ȥ)��
��m��3ʱ���ı���PBACΪƽ���ı��Σ�
�����ı���PABCΪƽ���ı��Σ�����BC��x�ᣬ
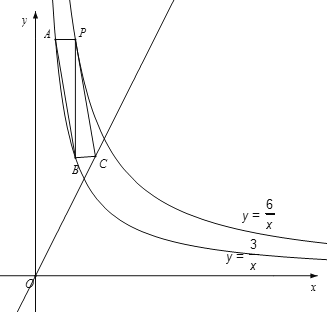
��C��������Ϊ![]() ��
��
��y��![]() ����y��2x��C(
����y��2x��C(![]() ��
��![]() )��
)��
��ʱBC��![]() ��m��
��m��
��BC��PA����![]() ��m��
��m��![]() ��
��
��ã�m��1��m����1(��ȥ)��
����PACBΪƽ���ı��Σ�����AC��BP��y�ᣬ
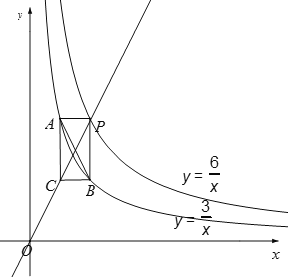
���C(![]() ��
��![]() )��
)��
����y��2x����![]() ��2��
��2��![]() ��
��
���m��![]() ��m����
��m����![]() (��ȥ)��
(��ȥ)��
���ϣ�m��3��1��![]() ʱ���Ե�P��A��B��CΪ������ı���Ϊƽ���ı���.
ʱ���Ե�P��A��B��CΪ������ı���Ϊƽ���ı���.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�������ߣ�y=��x��x��3����0��x��3������ΪC1������x�ύ�ڵ�O��A1����C1�Ƶ�A1��ת180���C2����x���ڵ�A2����C2�Ƶ�A2��ת180���C3����x���ڵ�A3������˽�����ȥ��ֱ����C17.
��1�����![]() ������________
������________
��2����P��50��m���ڵ�17��������C17�ϣ���m=_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽���һ�ΰ��꼶��ѧ����ɼ�����������ȡ��40��ѧ���ijɼ�����ͳ�Ʒ�������40��ѧ���ijɼ��������£�
55 62 67 53 58 83 87 64 68 85
60 94 81 98 51 83 78 77 66 71
91 72 63 75 88 73 52 71 79 63
74 67 78 61 97 76 72 77 79 71
��1�������������ʵ����飬����Ƶ���ֲ�����
�� �� | �� �� | �� �� | �� �� | �� �� | �� �� |
Ƶ �� | �� �� | �� �� | �� �� | �� �� | �� �� |
��2������Ƶ���ֲ���������Ƶ��ֱ��ͼ��
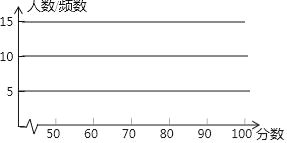
��3����ͼ���Կ�������40��ѧ���ijɼ����ֲ���ʲô��Χ�ڣ��������ĸ���Χ��������ࣿ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ϊ���������Լ��ˮ�����÷ֶμƷѵķ������¼���ÿ����ͥ��ˮ�ѣ�����ˮ��������30������ʱ����2Ԫ/�����Ʒѣ�����ˮ������30������ʱ�����е�30��������2Ԫ/�������շѣ��������ְ�2.5Ԫ/�����Ʒѣ���ÿ����ͥ����ˮ��Ϊx�����ף�
��1����x������30ʱ��Ӧ�ն���ˮ�ѣ���x�Ĵ���ʽ��ʾ������x����30ʱ��Ӧ�ն���ˮ�ѣ���x�Ĵ���ʽ��ʾ����
��2��С�������·���ˮ20�����ף����·���ˮ36�����ף����С������һ��������������һ��Ӧ������Ԫˮ�ѣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
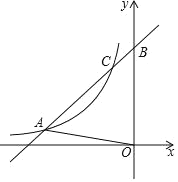
����Ŀ����ͼ��һ�κ���y1��kx+b��k��0����ͼ���뷴��������y2��![]() ��m��0��x��0����ͼ���ڵ�A����3��1���͵�C����y�ύ�ڵ�B����AOB�������6��
��m��0��x��0����ͼ���ڵ�A����3��1���͵�C����y�ύ�ڵ�B����AOB�������6��
��1������������һ�κ����Ľ���ʽ��
��2����x��0ʱ���Ƚ�y1��y2�Ĵ�С��
��3������P��x��y��Ҳ�ڷ���������y2��![]() ��ͼ���ϣ�����4��x����
��ͼ���ϣ�����4��x����![]() ʱ������ֵy��ȡֵ��Χ��
ʱ������ֵy��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��˾���ڼ�ʻ����ʱ�����ֽ������������ɲ����Ҫһ��ʱ�䣬���ʱ��з�Ӧʱ�䣮֮�������ʻһ�ξ��룮���ǰ�˾���ӷ��ֽ������������ֹͣ����ʻ����ξ������ɲ��������(��ͼ)��
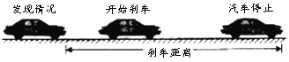
��֪������ɲ������![]() (��λ����)�복��
(��λ����)�복��![]() (��λ���ף���)֮�������¹�ϵ��
(��λ���ף���)֮�������¹�ϵ��![]() ������
������![]() Ϊ˾���ķ�Ӧʱ��(��λ����) ��
Ϊ˾���ķ�Ӧʱ��(��λ����) ��![]() Ϊ�ƶ�ϵ����ij����Ϊ����˾�����ƺ�ɲ������ı仯����ij���ͺŵ��������������������ݳ����ԣ���֪���ͺ��������ƶ�ϵ��
Ϊ�ƶ�ϵ����ij����Ϊ����˾�����ƺ�ɲ������ı仯����ij���ͺŵ��������������������ݳ����ԣ���֪���ͺ��������ƶ�ϵ��![]() �������־Ը����δ����ʱ�ķ�Ӧʱ��
�������־Ը����δ����ʱ�ķ�Ӧʱ��![]() �룮
�룮
��1����־Ը��δ���ƣ��ҳ���Ϊ16�ף��룬���������ɲ������Ϊ �� ��
��2����־Ը���ں���һƿơ�ư�Сʱ����16�ף�����ٶȼݳ���ʻ�����ɲ������Ϊ59.2�ף���ʱ��־Ը�ߵķ�Ӧʱ���� �룮
��3�������־Ը����10�ף���ij�����ʻ�����ƺ�Ӧʱ���ǵڣ�2��������������������ƺ��ɲ��������δ����ʱ��ɲ��������������˶��٣�
��4���������ʻ���ͺŵ�������16 �ף�����ٶ���ʻ, ������ǰ��46�״�ͣ��һ�����������㷴Ӧʱ����1. 3��.�����������Ƿ�ᷢ����β��? ��ͨ���������˵��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������60�����ˣ������ס������������ÿ��ÿ��ƽ���������������24�����������12������֪ÿ2�����������3������������һ�ף���Ӧ���������������������������������������������ʹÿ������������������պ����ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����E��F�ֱ���������ABCD�ı�CD��AD�ϵĵ㣬��CE=DF��AE��BF�ཻ�ڵ�O�������ĸ����ۣ���1��AE=BF����2��AE��BF����3��AO=OE����4��S��AOB=S�ı���DEOF��������ȷ���۵������ ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABΪ��ԲO��ֱ����CΪBA�ӳ�����һ�㣬CD�а�ԲO�ڵ�D������OD����BE��CD�ڵ�E������ԲO�ڵ�F����֪CE=12��BE=9,
(1)��֤����COD�ס�CBE��
(2)���ԲO�İ뾶�ij�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com