
【题目】如图,AB为半圆O的直径,C为BA延长线上一点,CD切半圆O于点D。连结OD,作BE⊥CD于点E,交半圆O于点F。已知CE=12,BE=9,
(1)求证:△COD∽△CBE;
(2)求半圆O的半径的长

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
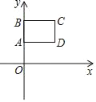
【题目】如图,在平面直角坐标系中,长方形ABCD的边AB在y轴正半轴上,顶点A的坐标为(0,2),设顶点C的坐标为(a,b).
(1)顶点B的坐标为 ,顶点D的坐标为 (用a或b表示);
(2)如果将一个点的横坐标作为x的值,纵坐标作为y的值,代入方程2x+3y=12成立,就说这个点的坐标是方程2x+3y=12的解.已知顶点B和D的坐标都是方程2x+3y=12的解,求a,b的值;
(3)在(2)的条件下,平移长方形ABCD,使点B移动到点D,得到新的长方形EDFG,
①这次平移可以看成是先将长方形ABCD向右平移 个单位长度,再向下平移 个单位长度的两次平移;
②若点P(m,n)是对角线BD上的一点,且点P的坐标是方程2x+3y=12的解,试说明平移后点P的对应点P′的坐标也是方程2x+3y=12的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店以4元/千克的价格购进一批水果,由于销售状况良好,该店又再次购进同一种水果,第二次进货价格比第一次每千克便宜了0.5元,所购水果重量恰好是第一次购进水果重量的2倍,这样该水果店两次购进水果共花去了2200元.
(1)该水果店两次分别购买了多少元的水果?
(2)在销售中,尽管两次进货的价格不同,但水果店仍以相同的价格售出,若第一次购进的水果有3%的损耗,第二次购进的水果有5%的损耗,该水果店希望售完这些水果获利不低于1244元,则该水果每千克售价至少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
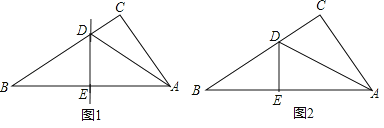
【题目】小王剪了两张直角三角形纸片,进行了如下的操作:
(1)如图1,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE,若AC=6cm,BC=8cm,求CD的长.
(2)如图2,小王拿出另一张Rt△ABC纸片,将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,若AC=6cm,BC=8cm,求CD的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.

(1)求证:EG=CG;
(2)将图①中△BEF绕B点逆时针旋转45°,如图②所示,取DF中点G,连接EG,CG.
问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
(3)将图①中△BEF绕B点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?通过观察你还能得出什么结论(均不要求证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们学过二次函数的图象的平移,如:将二次函数![]() 的图象向左平移2个单位,再向下平移4个单位,所图象的函数表达式是
的图象向左平移2个单位,再向下平移4个单位,所图象的函数表达式是![]() .类比二次函数的图象的平移,我们对反比例函数的图象作类似的变换:
.类比二次函数的图象的平移,我们对反比例函数的图象作类似的变换:
(1)将![]() 的图象向右平移1个单位,所得图象的函数表达式为_______,再向上平移1个单位,所得图象的函数表达式为_________;
的图象向右平移1个单位,所得图象的函数表达式为_______,再向上平移1个单位,所得图象的函数表达式为_________;
(2)函数![]() 的图象可由
的图象可由![]() 的图象向____平移____个单位得到;
的图象向____平移____个单位得到; ![]() 的图象可由哪个反比例函数的图象经过怎样的变换得到?
的图象可由哪个反比例函数的图象经过怎样的变换得到?
(3)一般地,函数![]() (
(![]() ,且
,且![]() )的图象可由哪个反比例函数的图象经过和怎样的变换得到?
)的图象可由哪个反比例函数的图象经过和怎样的变换得到?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,E是AD的中点,延长CB到点F,使![]() ,连接BE、AF.
,连接BE、AF.
(1)完成画图并证明四边形AFBE是平行四边形;
(2)若AB=6,AD=8,∠C=60°,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一棵树高h(m)与生长时间n(年)之间有一定关系,请你根据下表中数据,写出h(m)与n(年)之间的关系式:_____.
n/年 | 2 | 4 | 6 | 8 | … |
h/m | 2.6 | 3.2 | 3.8 | 4.4 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:
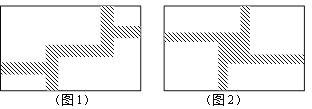
【题目】(1)如图1,在一块宽为12m,长为20m的矩形地面上修筑同样宽的道路,余下的部分种上草坪.要使草坪的面积为180m2,求道路的宽;
(2)现在对该矩形区域进行改造,如图2,在正中央建一个与矩形的边互相平行的正方形观赏亭,观赏亭的四边连接四条与矩形的边互相平行的且宽度相等的道路,已知道路的宽为正方形边长的![]() .若道路与观赏亭的面积之和是矩形面积的
.若道路与观赏亭的面积之和是矩形面积的![]() ,求道路的宽.
,求道路的宽.
【答案】(1)道路宽为2米;(2)道路的宽为1米.
【解析】试题分析:(1)设道路宽为x米,利用平移把不规则的图形变为规则图形,如此一来,所有草坪面积之和就变为了(20﹣x)(12﹣x)米2,进而即可列出方程,求出答案;
(2)设道路的宽为x米,则正方形边长为4x,根据道路与观赏亭的面积之和是矩形面积的![]() ,列方程求解即可.
,列方程求解即可.
试题解析:解:(1)设道路宽为x米,
根据题意得:(20﹣x)(12﹣x)=180
解得:x1=30(舍去),x2=2
答:道路宽为2米;
(2)设道路的宽为x米,
则可列方程:x(12-4x)+x(20-4x)+16x2=![]() ×20×12,
×20×12,
即:x2+4x-5=0,
解得:x1=1,x2=-5(舍去),
答:道路的宽为1米.
点睛:考查了一元二次方程的应用,这类题目体现了数形结合的思想,需利用平移把不规则的图形变为规则图形,进而即可列出方程,求出答案.另外还要注意解的合理性,从而确定取舍.
【题型】解答题
【结束】
10
【题目】如图1是一个三棱柱包装盒,它的底面是边长为10cm的正三角形,三个侧面都是矩形.现将宽为15cm的彩色矩形纸带AMCN裁剪成一个平行四边形ABCD(如图2),然后用这条平行四边形纸带按如图3的方式把这个三棱柱包装盒的侧面进行包贴(要求包贴时没有重叠部分),纸带在侧面缠绕三圈,正好将这个三棱柱包装盒的侧面全部包贴满.在图3中,将三棱柱沿过点A的侧棱剪开,得到如图4的侧面展开图.为了得到裁剪的角度,我们可以根据展开图拼接出符合条件的平行四边形进行研究.
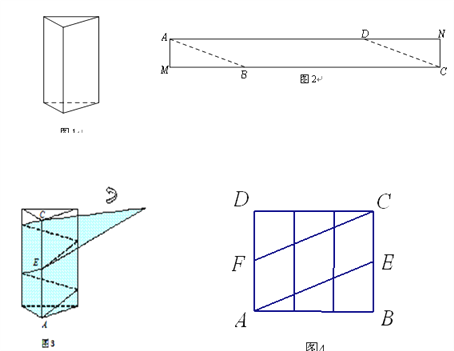
(1)请在图4中画出拼接后符合条件的平行四边形;
(2)请在图2中,计算裁剪的角度(即∠ABM的度数).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com