
【题目】我们学过二次函数的图象的平移,如:将二次函数![]() 的图象向左平移2个单位,再向下平移4个单位,所图象的函数表达式是
的图象向左平移2个单位,再向下平移4个单位,所图象的函数表达式是![]() .类比二次函数的图象的平移,我们对反比例函数的图象作类似的变换:
.类比二次函数的图象的平移,我们对反比例函数的图象作类似的变换:
(1)将![]() 的图象向右平移1个单位,所得图象的函数表达式为_______,再向上平移1个单位,所得图象的函数表达式为_________;
的图象向右平移1个单位,所得图象的函数表达式为_______,再向上平移1个单位,所得图象的函数表达式为_________;
(2)函数![]() 的图象可由
的图象可由![]() 的图象向____平移____个单位得到;
的图象向____平移____个单位得到; ![]() 的图象可由哪个反比例函数的图象经过怎样的变换得到?
的图象可由哪个反比例函数的图象经过怎样的变换得到?
(3)一般地,函数![]() (
(![]() ,且
,且![]() )的图象可由哪个反比例函数的图象经过和怎样的变换得到?
)的图象可由哪个反比例函数的图象经过和怎样的变换得到?
科目:初中数学 来源: 题型:
【题目】如图1,在综合实践活动中,同学们制作了两块直角三角形硬纸板,一块含有30°角,一块含有45°角,并且有一条直角边是相等的.现将含45°角的直角三角形硬纸板重叠放在含30°角的直角三角形硬纸板上,让它们的直角完全重合.如图2,若相等的直角边AC长为12cm,求另一条直角边没有重叠部分BD的长(结果用根号表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边三角形ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ.
(1)求证:△ABP≌△ACQ;
(2)请判断△APQ是什么三角形,试说明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数学活动课中,小敏为了测量校园内旗杆CD的高度,先在教学楼的底端A点处,观测到旗杆顶端C的仰角∠CAD=60°,然后爬到教学楼上的B处,观测到旗杆底端D的俯角是30°,已知教学楼AB高4米.

(1)求教学楼与旗杆的水平距离AD;(结果保留根号)
(2)求旗杆CD的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为半圆O的直径,C为BA延长线上一点,CD切半圆O于点D。连结OD,作BE⊥CD于点E,交半圆O于点F。已知CE=12,BE=9,
(1)求证:△COD∽△CBE;
(2)求半圆O的半径的长

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为二次函数y=ax2+bx+c的图象,在下列说法中:
①ac<0;
②方程ax2+bx+c=0的根是x1=﹣1,x2=3;
③a+b+c>0;
④当x>1时,y随着x的增大而增大.
正确的说法有________.(请写出所有正确的序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB.
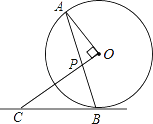
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为![]() ,OP=1,求BC的长.
,OP=1,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是△ABC的角平分线,点E、F分别在边BC、AB上,且DE∥AB,∠DEF=∠A.
(1)求证:BE=AF;
(2)设BD与EF交于点M,联结AE交BD于点N,求证:BNMD=BDND.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂计划生产A、B两种产品共50件,需购买甲、乙两种材料.生产一件A产品需甲种材料30千克、乙种材料10千克;生产一件B产品需甲、乙两种材料各20千克.经测算,购买甲、乙两种材料各1千克共需资金40元,购买甲种材料2千克和乙种材料3千克共需资金105元.
(1)甲、乙两种材料每千克分别是多少元?
(2)现工厂用于购买甲、乙两种材料的资金不超过38000元,且生产B产品不少于28件,问符合条件的生产方案有哪几种?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com