
����Ŀ��ij�����ƻ�����A��B���ֲ�Ʒ��50�����蹺��ס������ֲ��ϣ�����һ��A��Ʒ����ֲ���30ǧ�ˡ����ֲ���10ǧ�ˣ�����һ��B��Ʒ��ס������ֲ��ϸ�20ǧ�ˣ������㣬����ס������ֲ��ϸ�1ǧ�˹����ʽ�40Ԫ��������ֲ���2ǧ�˺����ֲ���3ǧ�˹����ʽ�105Ԫ��
��1���ס������ֲ���ÿǧ�˷ֱ��Ƕ���Ԫ��
��2���ֹ������ڹ���ס������ֲ��ϵ��ʽ���38000Ԫ��������B��Ʒ������28�����ʷ��������������������ļ��֣�
���𰸡���1���ס������ֲ���ÿǧ�˷ֱ���15��25Ԫ
��2������������3�֣���һ�֣�A��Ʒ20����B��Ʒ30��
�ڶ��֣�A��Ʒ21����B��Ʒ29��
�����֣�A��Ʒ22����B��Ʒ28��
��������
��1�����ȸ���������ס������ֲ���ÿǧ�˷ֱ���x,yԪ�����������з�����⼴��;
��2�����ȸ���������A���ֲ�Ʒ�ֱ�Ϊm�������������г�����ʽ����������⼴��.
��1����:��ס������ֲ���ÿǧ�˷ֱ���x,yԪ
��������ɵã�![]()
���![]()
��2����A���ֲ�Ʒ�ֱ�Ϊm������B�в�ƷΪ![]()
��������ɵã�![]()
��ã�![]() ����
����![]()
��m��ȡֵΪ��20��21��22
���Կɵ�����������3�֣���һ�֣�A��Ʒ20����B��Ʒ30��
�ڶ��֣�A��Ʒ21����B��Ʒ29��
�����֣�A��Ʒ22����B��Ʒ28��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ѧ�����κ�����ͼ���ƽ�ƣ��磺�����κ���![]() ��ͼ������ƽ��2����λ��������ƽ��4����λ����ͼ��ĺ�������ʽ��
��ͼ������ƽ��2����λ��������ƽ��4����λ����ͼ��ĺ�������ʽ��![]() .��ȶ��κ�����ͼ���ƽ�ƣ����ǶԷ�����������ͼ�������Ƶı任��
.��ȶ��κ�����ͼ���ƽ�ƣ����ǶԷ�����������ͼ�������Ƶı任��
��1����![]() ��ͼ������ƽ��1����λ������ͼ��ĺ�������ʽΪ_______��������ƽ��1����λ������ͼ��ĺ�������ʽΪ_________��
��ͼ������ƽ��1����λ������ͼ��ĺ�������ʽΪ_______��������ƽ��1����λ������ͼ��ĺ�������ʽΪ_________��
��2������![]() ��ͼ�����
��ͼ�����![]() ��ͼ����____ƽ��____����λ�õ���
��ͼ����____ƽ��____����λ�õ��� ![]() ��ͼ������ĸ�������������ͼ�������ı任�õ���
��ͼ������ĸ�������������ͼ�������ı任�õ���
��3��һ��أ�����![]() ��
��![]() ����
����![]() ����ͼ������ĸ�������������ͼ���������ı任�õ���
����ͼ������ĸ�������������ͼ���������ı任�õ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������˾��ÿ100ǧ��150Ԫ��ȡ��ѣ����������˾��ÿ100ǧ��50Ԫ��ȡ��ѣ����ӹ�����800Ԫ![]() ���ó����Ϊxǧ��
���ó����Ϊxǧ��![]() ���üס������ҹ�˾���������÷ֱ�Ϊ
���üס������ҹ�˾���������÷ֱ�Ϊ![]() Ԫ��
Ԫ��![]() Ԫ
Ԫ![]()
![]() �ֱ����
�ֱ����![]() ��
��![]() ��x֮��ĺ�����ϵʽ��
��x֮��ĺ�����ϵʽ��
![]() �ж�x��ʲô��Χ�ڣ������ҹ�˾���������ñ����ü�˾�����������٣�
�ж�x��ʲô��Χ�ڣ������ҹ�˾���������ñ����ü�˾�����������٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ĸ�ڹ���������ijУ�ڱ�Уѧ��������һ�γ������飬���ѵ������ֳ��������ͣ�A����֪����һ����ĸ�ڵģ�B��֪����û���κ��ж��ģ�C��֪�����ʺ�ĸ�ģ���ͼ�Ǹ��ݵ��������Ƶ�ͳ��ͼ�����֣�������ͼ���ṩ����Ϣ���ش��������⣺
����֪A��ѧ��ռ������ѧ��������30%������ѧ���ж����ˣ�
�ڼ���B��ѧ�������������ݼ�������ȫͳ��ͼ��
�������У����ѧ��2000�ˣ��Թ������ѧУѧ�����ж�����֪��ĸ�ڲ��ʺ���ĸ�ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ1����һ���Ϊ12m����Ϊ20m�ľ��ε���������ͬ�����ĵ�·�����µIJ������ϲ�ƺ��Ҫʹ��ƺ�����Ϊ180m2�����·�Ŀ���
��2�����ڶԸþ���������и��죬��ͼ2���������뽨һ������εı���ƽ�е������ι���ͤ������ͤ���ı�������������εı���ƽ�е��ҿ�����ȵĵ�·����֪��·�Ŀ�Ϊ�����α߳���![]() ������·�����ͤ�����֮���Ǿ��������
������·�����ͤ�����֮���Ǿ��������![]() �����·�Ŀ���
�����·�Ŀ���
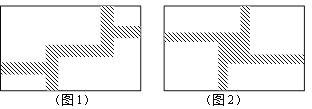
���𰸡���1����·��Ϊ2������2����·�Ŀ�Ϊ1�ף�
�������������������1�����·��Ϊx�ף�����ƽ�ưѲ������ͼ�α�Ϊ����ͼ�Σ����һ�������в�ƺ���֮�;ͱ�Ϊ�ˣ�20��x����12��x����2�����������г����̣��������
��2�����·�Ŀ�Ϊx�ף��������α߳�Ϊ4x�����ݵ�·�����ͤ�����֮���Ǿ��������![]() ���з�����⼴����
���з�����⼴����
����������⣺��1�����·��Ϊx�ף�
����������20��x����12��x��=180
��ã�x1=30����ȥ����x2=2
�𣺵�·��Ϊ2�ף�
��2�����·�Ŀ�Ϊx�ף�
����з��̣�x��12-4x��+x��20-4x��+16x2=![]() ��20��12��
��20��12��
����x2+4x-5=0��
��ã�x1=1��x2=-5����ȥ����
�𣺵�·�Ŀ�Ϊ1�ף�
�㾦��������һԪ���η��̵�Ӧ�ã�������Ŀ���������ν�ϵ�˼�룬������ƽ�ưѲ������ͼ�α�Ϊ����ͼ�Σ����������г����̣�����𰸣����Ҫע���ĺ����ԣ��Ӷ�ȷ��ȡ�ᣮ
�����͡������
��������
10
����Ŀ����ͼ1��һ����������װ�У����ĵ����DZ߳�Ϊ10cm���������Σ��������涼�Ǿ��Σ��ֽ���Ϊ15cm�IJ�ɫ����ֽ��AMCN�ü���һ��ƽ���ı���ABCD����ͼ2����Ȼ��������ƽ���ı���ֽ������ͼ3�ķ�ʽ�������������װ�еIJ�����а�����Ҫ�����ʱû���ص����֣���ֽ���ڲ��������Ȧ�����ý������������װ�еIJ���ȫ������������ͼ3�У����������ع���A�IJ���������õ���ͼ4�IJ���չ��ͼ.Ϊ�˵õ��ü��ĽǶ�,���ǿ��Ը���չ��ͼƴ�ӳ�����������ƽ���ı��ν����о�.
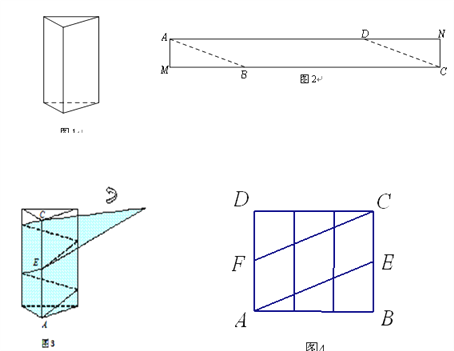
��1������ͼ4�л���ƴ�Ӻ����������ƽ���ı��Σ�
��2������ͼ2�У�����ü��ĽǶȣ�����ABM�Ķ�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() �ֱ���ֱ��AB��
�ֱ���ֱ��AB��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ��
��![]() ,
,![]() ��
��![]() ������
������![]() ��ƽ������
��ƽ������![]() ��ƽ���߽��ڵ�
��ƽ���߽��ڵ�![]() ,��ֱ��
,��ֱ��![]() ���ڵ�
���ڵ�![]() ,
,![]() ��
��![]() �ڵ�
�ڵ�![]() ,������˵���д������( )
,������˵���д������( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Ϊ�˼��������ľ����ſ��Ƿ�ϸ�ij����ĸ�ѧϰС�������ǰ��ϸ���ֱ������½�������в����ж��ſ��Ƿ�ϸ���ǣ� ��

A. AB=CD��AD=BC��AC=BD B. AC=BD����B=��C=90�� C. AB=CD����B=��C=90�� D. AB=CD��AC=BD
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����10������Rt��ABC�У���BAC=![]() ,D��BC���е㣬E��AD���е�������A��AF��BC��BE���ӳ����ڵ�F��
,D��BC���е㣬E��AD���е�������A��AF��BC��BE���ӳ����ڵ�F��

��1����֤����AEF����DEB��
��2��֤���ı���ADCF�����Σ�
��3����AC=4��AB=5��������ADCFD �������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������ĺ�����װ�кڡ���������ɫ����40ֻ����Щ�����ɫ��������ȫ��ͬ��Сӱ������ʵ�飬���Ⱥ����Ӻ������������һֻ�������ɫ���ٰ���Żغ����У������ظ��������̣��±���ʵ���е�һ��ͳ�����ݣ�
����Ĵ���n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
��������Ĵ���m | 65 | 124 | 178 | 302 | 481 | 599 | 1803 |
���������Ƶ�� | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
��1������ƣ���n�ܴ�ʱ�����������Ƶ�ʽ���ӽ��� ��������ȷ��0.1��
��2�����Ӻ������������һֻ������������ĸ��ʵĹ���ֵΪ�� ����
��3���Թ��������ڡ���������ɫ������ж���ֻ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com