
【题目】在等边三角形ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ.
(1)求证:△ABP≌△ACQ;
(2)请判断△APQ是什么三角形,试说明你的结论.

【答案】(1)证明见解析;(2) △APQ是等边三角形.
【解析】(1)由△ABC是等边三角形,可得AB=AC,结合已知∠ABP=∠ACQ,BP=CQ,利用SAS,即可得出△ABP≌△ACQ;
(2)由△ABP≌△ACQ,可得AP=AQ,∠BAP=∠CAQ,再由∠BAP+∠CAP=60°,可得∠PAQ=60°,即可得出△APQ是等边三角形.
(1)∵△ABC为等边三角形,
∴AB=AC,
又∵∠ABP=∠ACQ,BP=CQ,
∴△ABP≌△ACQ(SAS);
(2)△APQ为等边三角形.
理由如下:∵△ABP≌△ACQ,
∴∠BAP=∠CAQ,AP=AQ,
∵△ABC为等边三角形,∴∠BAC=60°,
∴∠BAP+∠CAP=60°,∴∠PAQ=∠CAQ+∠CAP=60°,
∴△APQ是等边三角形.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两人共同计算一道整式乘法:(2x+a)(3x+b),由于甲抄错了第一个多项式中a的符号,得到的结果为6x2+11x-10;由于乙漏抄了第二个多项式中的x的系数,得到的结果为2x2-9x+10.请你计算出a,b的值各是多少,并写出这道整式乘法的正确结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从广州去某市,可乘坐普通列车或高铁,已知高铁的行驶路程是400千米,普通列车的行驶路程是高铁的行驶路程的1.3倍.
(1)求普通列车的行驶路程;
(2)若高铁的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求高铁的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:A(0,1),B(2,0),C(4,3)
(1)在直角坐标系中描出各点,画出△ABC.
(2)求△ABC的面积;
(3)设点P在坐标轴上,且△ABP与△ABC的面积相等,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店以4元/千克的价格购进一批水果,由于销售状况良好,该店又再次购进同一种水果,第二次进货价格比第一次每千克便宜了0.5元,所购水果重量恰好是第一次购进水果重量的2倍,这样该水果店两次购进水果共花去了2200元.
(1)该水果店两次分别购买了多少元的水果?
(2)在销售中,尽管两次进货的价格不同,但水果店仍以相同的价格售出,若第一次购进的水果有3%的损耗,第二次购进的水果有5%的损耗,该水果店希望售完这些水果获利不低于1244元,则该水果每千克售价至少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.
(1)求证:四边形ACDF是平行四边形;
(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王剪了两张直角三角形纸片,进行了如下的操作:
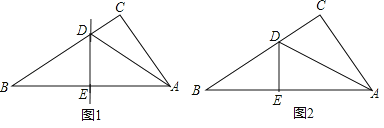
(1)如图1,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE,若AC=6cm,BC=8cm,求CD的长.
(2)如图2,小王拿出另一张Rt△ABC纸片,将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,若AC=6cm,BC=8cm,求CD的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们学过二次函数的图象的平移,如:将二次函数![]() 的图象向左平移2个单位,再向下平移4个单位,所图象的函数表达式是
的图象向左平移2个单位,再向下平移4个单位,所图象的函数表达式是![]() .类比二次函数的图象的平移,我们对反比例函数的图象作类似的变换:
.类比二次函数的图象的平移,我们对反比例函数的图象作类似的变换:
(1)将![]() 的图象向右平移1个单位,所得图象的函数表达式为_______,再向上平移1个单位,所得图象的函数表达式为_________;
的图象向右平移1个单位,所得图象的函数表达式为_______,再向上平移1个单位,所得图象的函数表达式为_________;
(2)函数![]() 的图象可由
的图象可由![]() 的图象向____平移____个单位得到;
的图象向____平移____个单位得到; ![]() 的图象可由哪个反比例函数的图象经过怎样的变换得到?
的图象可由哪个反比例函数的图象经过怎样的变换得到?
(3)一般地,函数![]() (
(![]() ,且
,且![]() )的图象可由哪个反比例函数的图象经过和怎样的变换得到?
)的图象可由哪个反比例函数的图象经过和怎样的变换得到?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲汽车出租公司按每100千米150元收取租车费:乙汽车出租公司按每100千米50元收取租车费,另加管理费800元![]() 设用车里程为x千米
设用车里程为x千米![]() 租用甲、乙两家公司的汽车费用分别为
租用甲、乙两家公司的汽车费用分别为![]() 元、
元、![]() 元
元![]()
![]() 分别求出
分别求出![]() 、
、![]() 与x之间的函数关系式;
与x之间的函数关系式;
![]() 判断x在什么范围内,租用乙公司的汽车费用比租用甲公司的汽车费用少?
判断x在什么范围内,租用乙公司的汽车费用比租用甲公司的汽车费用少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com