
【题目】如图,BD是△ABC的角平分线,点E、F分别在边BC、AB上,且DE∥AB,∠DEF=∠A.
(1)求证:BE=AF;
(2)设BD与EF交于点M,联结AE交BD于点N,求证:BNMD=BDND.

【答案】(1)见解析;(2)见解析
【解析】试题分析:(1)先证明四边形ADEF为平行四边形得到AF=DE,再证明∠DBE=∠BDE得到BE=DE,则BE=AF;
(2)如图,根据平行线分线段成比例定理,由EF∥AC得到AF:AB=DM:BD等量代换得DE:AB=DM:BD,再由DE∥AB得到DE:AB=DN:BN,则DM:BD=DN:BN,然后利用比例的性质即可得到结论.
试题解析:
证明:(1)∵DE∥AB,
∴∠A+∠ADE=180°,
∵∠DEF=∠A,
∴∠DEF+∠ADE=180°,
∴EF∥AD,
∴四边形ADEF为平行四边形,
∴AF=DE,
∵BD是△ABC的角平分线,
∴∠DBE=∠ABD,
∵DE∥AB,
∴∠ABD=∠BDE,
∴∠DBE=∠BDE,
∴BE=DE,
∴BE=AF;
(2)如图,
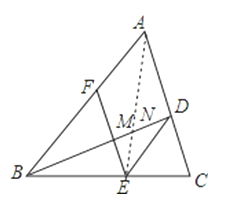
∵EF∥AC,
∴AF:AB=DM:BD,
∵AF=DE,
∴DE:AB=DM:BD,
∵DE∥AB,
∴DE:AB=DN:BN,
∴DM:BD=DN:BN,
即BN·MD=BD·ND.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案科目:初中数学 来源: 题型:
【题目】已知:A(0,1),B(2,0),C(4,3)
(1)在直角坐标系中描出各点,画出△ABC.
(2)求△ABC的面积;
(3)设点P在坐标轴上,且△ABP与△ABC的面积相等,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们学过二次函数的图象的平移,如:将二次函数![]() 的图象向左平移2个单位,再向下平移4个单位,所图象的函数表达式是
的图象向左平移2个单位,再向下平移4个单位,所图象的函数表达式是![]() .类比二次函数的图象的平移,我们对反比例函数的图象作类似的变换:
.类比二次函数的图象的平移,我们对反比例函数的图象作类似的变换:
(1)将![]() 的图象向右平移1个单位,所得图象的函数表达式为_______,再向上平移1个单位,所得图象的函数表达式为_________;
的图象向右平移1个单位,所得图象的函数表达式为_______,再向上平移1个单位,所得图象的函数表达式为_________;
(2)函数![]() 的图象可由
的图象可由![]() 的图象向____平移____个单位得到;
的图象向____平移____个单位得到; ![]() 的图象可由哪个反比例函数的图象经过怎样的变换得到?
的图象可由哪个反比例函数的图象经过怎样的变换得到?
(3)一般地,函数![]() (
(![]() ,且
,且![]() )的图象可由哪个反比例函数的图象经过和怎样的变换得到?
)的图象可由哪个反比例函数的图象经过和怎样的变换得到?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知AB=AC,∠BAC=90°,AH是△ABC的高,AH=4 cm,BC=8 cm,直线CM⊥BC,动点D从点C开始沿射线CB方向以每秒3厘米的速度运动,动点E也同时从点C开始在直线CM上以每秒1厘米的速度向远离C点的方向运动,连接AD、AE,设运动时间为t(t>0)秒.
(1)请直接写出CD、CE的长度(用含有t的代数式表示):CD= cm,CE= cm;
(2)当t为多少时,△ABD的面积为12 cm2?
(3)请利用备用图探究,当t为多少时,△ABD≌△ACE?并简要说明理由.
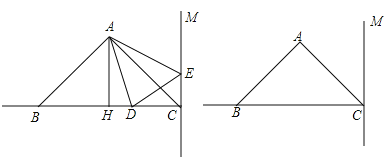
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一棵树高h(m)与生长时间n(年)之间有一定关系,请你根据下表中数据,写出h(m)与n(年)之间的关系式:_____.
n/年 | 2 | 4 | 6 | 8 | … |
h/m | 2.6 | 3.2 | 3.8 | 4.4 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知AB=AC,∠BAC=90°,AH是△ABC的高,AH=4 cm,BC=8 cm,直线CM⊥BC,动点D从点C开始沿射线CB方向以每秒3厘米的速度运动,动点E也同时从点C开始在直线CM上以每秒1厘米的速度向远离C点的方向运动,连接AD、AE,设运动时间为t(t>0)秒.
(1)请直接写出CD、CE的长度(用含有t的代数式表示):CD= cm,CE= cm;
(2)当t为多少时,△ABD的面积为12 cm2?
(3)请利用备用图探究,当t为多少时,△ABD≌△ACE?并简要说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲汽车出租公司按每100千米150元收取租车费:乙汽车出租公司按每100千米50元收取租车费,另加管理费800元![]() 设用车里程为x千米
设用车里程为x千米![]() 租用甲、乙两家公司的汽车费用分别为
租用甲、乙两家公司的汽车费用分别为![]() 元、
元、![]() 元
元![]()
![]() 分别求出
分别求出![]() 、
、![]() 与x之间的函数关系式;
与x之间的函数关系式;
![]() 判断x在什么范围内,租用乙公司的汽车费用比租用甲公司的汽车费用少?
判断x在什么范围内,租用乙公司的汽车费用比租用甲公司的汽车费用少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】母亲节过后,永川区某校在本校学生中做了一次抽样调查,并把调查结果分成三种类型:A.已知道哪一天是母亲节的;B.知道但没有任何行动的;C.知道并问候母亲的.如图是根据调查结果绘制的统计图(部分),根据图中提供的信息,回答下列问题:
①已知A类学生占被调查学生人数的30%,则被调查学生有多少人?
②计算B类学生的人数并根据计算结果补全统计图;
③如果该校共有学生2000人,试估计这个学校学生中有多少人知道母亲节并问候了母亲.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)在Rt△ABC中,∠BAC=![]() ,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.

(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCFD 的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com