
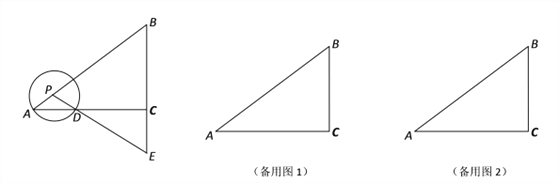
【题目】如图,已知在Rt△ABC中,∠ACB=90°,cosB=![]() ,BC=3,P是射线AB上的一个动点,以P为圆心,PA为半径的⊙P与射线AC的另一个交点为D,直线PD交直线BC于点E.
,BC=3,P是射线AB上的一个动点,以P为圆心,PA为半径的⊙P与射线AC的另一个交点为D,直线PD交直线BC于点E.
(1)当PA=1时,求CE的长;
(2)如果点P在边AB的上,当⊙P与以点C为圆心,CE为半径的⊙C内切时,求⊙P的半径;
(3)设线段BE的中点为Q,射线PQ与⊙P相交于点F,点P在运动过程中,当PE∥CF时,求AP的长.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】试题分析:(1)作PH⊥AC,垂足为H,由垂径定理可得AH=DH,由cosB=![]() BC=3,可得AB=5,AC=4,再由PH∥BC,可得
BC=3,可得AB=5,AC=4,再由PH∥BC,可得![]() ,代入数据求得PH=
,代入数据求得PH=![]() ,即可求得
,即可求得![]() ,由
,由![]() ,代入数据求得CE的长即可;(2)当⊙P与⊙C内切时,点C在⊙P内,可得点D在AC的延长线上,过点P作PG⊥AC,垂足为G,设PA=
,代入数据求得CE的长即可;(2)当⊙P与⊙C内切时,点C在⊙P内,可得点D在AC的延长线上,过点P作PG⊥AC,垂足为G,设PA=![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,根据
,根据![]() ,代入数据可得
,代入数据可得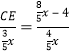 ,解得
,解得![]() ,因⊙P与⊙C内切,即可得
,因⊙P与⊙C内切,即可得![]() ,所以
,所以![]() ,即
,即![]() ,解得
,解得![]() ,
,![]() (舍去),即当⊙P与⊙C内切时,⊙P的半径为
(舍去),即当⊙P与⊙C内切时,⊙P的半径为![]() ;(3)先证明四边形PDCF是平行四边形,可得PF=CD,再分当点P在边AB的上和当点P在边AB的延长线上两种情况求AP的长.
;(3)先证明四边形PDCF是平行四边形,可得PF=CD,再分当点P在边AB的上和当点P在边AB的延长线上两种情况求AP的长.
试题解析:
(1)作PH⊥AC,垂足为H,∵PH过圆心,∴AH=DH
∵∠ACB=90°,∴PH∥BC, ∵cosB=![]() ,BC=3,∴AB=5,AC=4
,BC=3,∴AB=5,AC=4
∵PH∥BC,∴![]() ,∴
,∴![]() ,∴
,∴![]()
∴![]()
∴DC=![]() ,又∵
,又∵![]() ,∴
,∴![]() ,∴
,∴![]()
(2)当⊙P与⊙C内切时,点C在⊙P内,∴点D在AC的延长线上
过点P作PG⊥AC,垂足为G,设PA=![]() ,则
,则![]() ,
,![]()
![]() ,
,![]() ,∵
,∵![]() ,
,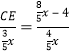 ,
,![]() …(1分)
…(1分)
∵⊙P与⊙C内切,∴![]()
∴![]()
∴![]() ,∴
,∴![]() ,
,![]() (舍去)
(舍去)
∴当⊙P与⊙C内切时,⊙P的半径为![]() .
.
(3)∵∠ABC+∠A=90゜,∠PEC+∠CDE=90゜,∠A=∠PDA,
∴∠ABC=∠PEC
∵∠ABC=∠EBP,
∴∠PEC=∠EBP,
∴PB=PE
∵点Q为线段BE的中点,
∴PQ⊥BC,∴PQ∥AC
∴当PE∥CF时,四边形PDCF是平行四边形,∴PF=CD
当点P在边AB的上时,![]() ,
,![]()
当点P在边AB的延长线上时,![]() ,
,![]()
综上所述,当PE∥CF时,AP的长为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】
乐天借到一本有72页的图书,要在10天之内读完,开始两天每天只读5页,那么以后几天里每天至少要读多少页?设以后几天里每天要读x页,所列不等式为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中.矩形OABC的对角线OB,AC相交于点D,且BE∥AC,AE∥OB.如果OA=3,OC=2,则经过点E的反比例函数解析式为( ) 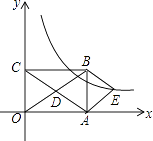
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,四边形ABCD四个顶点的坐标分别为A(﹣2,0),B(﹣1,2),C(3,3),D(4,0).
(1)画出四边形ABCD;
(2)把四边形ABCD向下平移4个单位长度,再向左平移2个单位长度得到四边形A′B′C′D′,画出四边形A′B′C′D′,并写出C′的坐标;
(3)求出四边形ABCD的面积.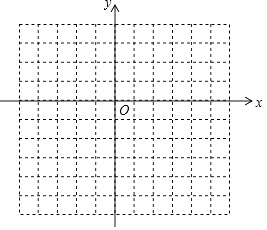
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校准备组织520名学生进行野外考察活动,行李共有240件.学校计划租用甲、乙两种型号的汽车共12辆,经了解,甲种汽车每辆最多能载50人和15件行李,乙种汽车每辆最多能载40人和25件行李.设租用甲种汽车![]() 辆,你认为下列符合题意的不等式组是( )
辆,你认为下列符合题意的不等式组是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形ABCD中,M为边AB上的点,且AM= ![]() BM,延长MB至点E,使ME=MC,连接EC,则点M到直线CE的距离是( )
BM,延长MB至点E,使ME=MC,连接EC,则点M到直线CE的距离是( ) 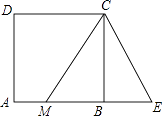
A.2
B.![]()
C.5
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列表格是二次函数y=ax2+bx+c(d≠0)的自变量x与函数y的一些对应值,由此可以判断方程ax2+bx+c=0(a≠0)的一个根在( )
x | 6.17 | 6.18 | 6.19 | 6.20 |
y=ax2+bx+c | ﹣0.03 | ﹣0.01 | 0.02 | 0.06 |
A.﹣0.01﹣0.02之间
B.0.02﹣0.06之间
C.6.17﹣6.18之间
D.6.18﹣6.19之间
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com