
【题目】如图,在边长为4的正方形ABCD中,M为边AB上的点,且AM= ![]() BM,延长MB至点E,使ME=MC,连接EC,则点M到直线CE的距离是( )
BM,延长MB至点E,使ME=MC,连接EC,则点M到直线CE的距离是( ) 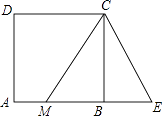
A.2
B.![]()
C.5
D.2 ![]()
【答案】D
【解析】解:如图,作MN⊥EC于N. 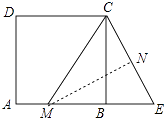
∵四边形ABCD是正方形,
∴AB=BC=CD=AD=4,∠ABC=90°,
∴AM= ![]() BM,
BM,
∴AM=1,BM=3,
在Rt△BCM中,CM=ME= ![]() =
= ![]() =5,
=5,
∴BE=5﹣3=2,
∴CE= ![]() =
= ![]() =2
=2 ![]()
∵ ![]() MECB=
MECB= ![]() CEMN,
CEMN,
∴MN= ![]() =
= ![]() =2
=2 ![]() ,
,
故选D.
【考点精析】本题主要考查了点到直线的距离和正方形的性质的相关知识点,需要掌握从直线外一点到这条直线的垂线段的长度叫做点到直线的距离;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:
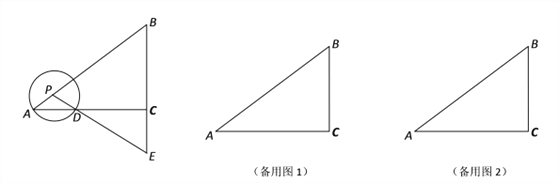
【题目】如图,已知在Rt△ABC中,∠ACB=90°,cosB=![]() ,BC=3,P是射线AB上的一个动点,以P为圆心,PA为半径的⊙P与射线AC的另一个交点为D,直线PD交直线BC于点E.
,BC=3,P是射线AB上的一个动点,以P为圆心,PA为半径的⊙P与射线AC的另一个交点为D,直线PD交直线BC于点E.
(1)当PA=1时,求CE的长;
(2)如果点P在边AB的上,当⊙P与以点C为圆心,CE为半径的⊙C内切时,求⊙P的半径;
(3)设线段BE的中点为Q,射线PQ与⊙P相交于点F,点P在运动过程中,当PE∥CF时,求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】8月25日,高德公司发布了《2015年第二季度中国主要城市交通分析报告》,在国内城市拥堵排行中,北京、杭州、广州位列前三,山城重庆排第九.为了解重庆市交通拥堵情况,经调查统计:菜园坝长江大桥上的车流速度V(单位:千米/时)是车流密度x(单位:辆/千米)的一次函数,且满足v=﹣ ![]() x+88(其中20≤x≤220).
x+88(其中20≤x≤220).
(1)在交通高峰时段,为使菜园坝长江大桥上车流速度不小于48千米/时且不大于60千米/时,应控制
菜园坝长江大桥上的车流密度在什么范围内?
(2)若规定车流量(单位:辆/时)是单位时间内通过桥上某观测点的车辆数.即:车流量=车流速度×车
流密度.那在(1)的条件下.菜园坝长江大桥上车流量的最大值是多少?
(3)当车流量为4680辆/时时,为了使桥上的更畅通,则桥上的车流密度应为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人共同解方程组![]() , 由于甲错了方程①中的a,得到方程组的解为
, 由于甲错了方程①中的a,得到方程组的解为![]() ;乙看错了方程②中的b,得到方程组的解为
;乙看错了方程②中的b,得到方程组的解为![]() ,
,
(1)求出a,b的值;
(2)求2a﹣3b+5的立方根;
(3)此方程组正确的解应该是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com