
【题目】8月25日,高德公司发布了《2015年第二季度中国主要城市交通分析报告》,在国内城市拥堵排行中,北京、杭州、广州位列前三,山城重庆排第九.为了解重庆市交通拥堵情况,经调查统计:菜园坝长江大桥上的车流速度V(单位:千米/时)是车流密度x(单位:辆/千米)的一次函数,且满足v=﹣ ![]() x+88(其中20≤x≤220).
x+88(其中20≤x≤220).
(1)在交通高峰时段,为使菜园坝长江大桥上车流速度不小于48千米/时且不大于60千米/时,应控制
菜园坝长江大桥上的车流密度在什么范围内?
(2)若规定车流量(单位:辆/时)是单位时间内通过桥上某观测点的车辆数.即:车流量=车流速度×车
流密度.那在(1)的条件下.菜园坝长江大桥上车流量的最大值是多少?
(3)当车流量为4680辆/时时,为了使桥上的更畅通,则桥上的车流密度应为多少?
【答案】
(1)解:由题意,得 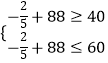 ,
,
解得:70≤x≤120.
故应控制大桥上的车流密度在70≤x≤120范围内
(2)解:设车流量y与x之间的关系式为y=vx,
当70≤x≤120时
y=(﹣ ![]() x+88)x=﹣
x+88)x=﹣ ![]() (x﹣110)2+4840,
(x﹣110)2+4840,
∴当x=110时,y最大=4840.
∴当车流密度是110辆/千米,车流量y取得最大值是每小时4840辆
(3)解:当y=4680时,即4680=﹣ ![]() (x﹣110)2+4840,
(x﹣110)2+4840,
解得:x=130,或x=90,
故当车流量为4680辆/时时,为了使桥上的更畅通,则桥上的车流密度应为130辆/千米,或90辆/千米
【解析】(1)根据题意得方程组即可得到结论;(2)设车流量y与x之间的关系式为y=vx,当70≤x≤120时求得函数关系,由函数的性质就可以求出结论;(3)当y=4680时,列方程即可得到结论.
【考点精析】解答此题的关键在于理解一元一次不等式组的应用的相关知识,掌握1、审:分析题意,找出不等关系;2、设:设未知数;3、列:列出不等式组;4、解:解不等式组;5、检验:从不等式组的解集中找出符合题意的答案;6、答:写出问题答案.


科目:初中数学 来源: 题型:
【题目】综合题。
(1)先化简,再求值:(x﹣2)(3x2﹣1)﹣12x( ![]() x2﹣
x2﹣ ![]() x﹣3),其中x=﹣
x﹣3),其中x=﹣ ![]()
(2)已知x2﹣5x=3,求2(x﹣1)(2x﹣1)﹣2(x+1)2+1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,四边形ABCD四个顶点的坐标分别为A(﹣2,0),B(﹣1,2),C(3,3),D(4,0).
(1)画出四边形ABCD;
(2)把四边形ABCD向下平移4个单位长度,再向左平移2个单位长度得到四边形A′B′C′D′,画出四边形A′B′C′D′,并写出C′的坐标;
(3)求出四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校准备组织520名学生进行野外考察活动,行李共有240件.学校计划租用甲、乙两种型号的汽车共12辆,经了解,甲种汽车每辆最多能载50人和15件行李,乙种汽车每辆最多能载40人和25件行李.设租用甲种汽车![]() 辆,你认为下列符合题意的不等式组是( )
辆,你认为下列符合题意的不等式组是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对于实数a,符号[a]表示不大于a的最大整数,例如:[4.7]=4,[﹣π]=﹣4,[3]=3,如果[ ![]() +1]=﹣5,则x的取值范围为 .
+1]=﹣5,则x的取值范围为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形ABCD中,M为边AB上的点,且AM= ![]() BM,延长MB至点E,使ME=MC,连接EC,则点M到直线CE的距离是( )
BM,延长MB至点E,使ME=MC,连接EC,则点M到直线CE的距离是( ) 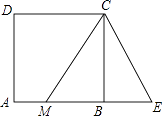
A.2
B.![]()
C.5
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人共同解方程组![]() , 由于甲看错了方程①中的a,得到方程组的解为
, 由于甲看错了方程①中的a,得到方程组的解为![]() ;乙看错了方程②中的b,得到方程组的解为
;乙看错了方程②中的b,得到方程组的解为![]() , 试计算a2012+(
, 试计算a2012+(![]() b)2013的值.
b)2013的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com