
【题目】过点(﹣1,7)的一条直线与x轴,y轴分别相交于点A,B,且与直线![]() y=-
y=-![]() x+1 平行.则在线段AB上,横、纵坐标都是整数的点的坐标是
x+1 平行.则在线段AB上,横、纵坐标都是整数的点的坐标是
【答案】(1,4),(3,1)
【解析】∵过点(﹣1,7)的一条直线与直线y=-![]() x+1平行,设直线AB为y=﹣
x+1平行,设直线AB为y=﹣ ![]() x+b;
x+b;
把(﹣1,7)代入y=﹣ ![]() x+b;得7=
x+b;得7= ![]() +b,
+b,
解得:b= ![]() ,
,
∴直线AB的解析式为y=﹣ ![]() x+
x+ ![]() ,
,
令y=0,得:0=﹣ ![]() x+
x+ ![]() ,
,
解得:x= ![]() ,
,
∴0<x< ![]() 的整数为:1、2、3;
的整数为:1、2、3;
把x等于1、2、3分别代入解析式得4、 ![]() 、1;
、1;
∴在线段AB上,横、纵坐标都是整数的点的坐标是(1,4),(3,1).
故答案为:(1,4),(3,1).
根据两直线平行,即两个一次函数的k值相等,设直线AB为y=﹣ ![]() x+b,再把(-1,7)代入解析式求出b的值,即可得出函数解析式,再根据y=0,求出x的值,得出自变量的取值范围,然后写出自变量的整数解,求出对应的函数值,即可求出横、纵坐标都是整数的点的坐标。
x+b,再把(-1,7)代入解析式求出b的值,即可得出函数解析式,再根据y=0,求出x的值,得出自变量的取值范围,然后写出自变量的整数解,求出对应的函数值,即可求出横、纵坐标都是整数的点的坐标。


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
【题目】2014年1月,国家发改委出台指导意见,要求2015年底前,所有城市原则上全面实行居民阶梯水价制度. 小军为了解市政府调整水价方案的社会反响,随机访问了自己居住在小区的部分居民,就“每月每户的用水量”和“调价对用水行为改变”两个问题进行调查,并把调查结果整理成下面的图1,图2.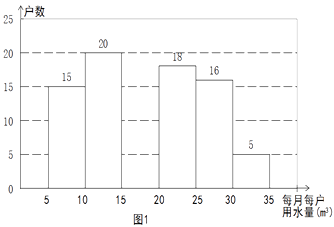

小军发现每月每户的用水量在5m3-35m3之间,有7户居民对用水价格调价涨幅抱无所谓,不用考虑用水方式的改变. 根据小军绘制的图表和发现的信息,完成下列问题:
(1)n = , 小明调查了户居民,并补全图1;
(2)每月每户用水量的中位数落在之间,众数落在之间;
(3)如果小明所在的小区有1200户居民,请你估计“视调价涨幅采取相应的用水方式改变”的居民户数有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若△ABC的三边a,b,c满足(ac)(a2+b2c2)=0,则△ABC是( )
A. 等腰三角形 B. 直角三角形
C. 等腰三角形或直角三角形 D. 等腰直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如右图,![]() 为等腰
为等腰![]() 的外接圆,直径
的外接圆,直径![]() ,
,![]() 为弧
为弧![]() 上任意一点(不与
上任意一点(不与![]() ,
,![]() 重合),直线
重合),直线![]() 交
交![]() 延长线于点
延长线于点![]() ,
,![]() 在点
在点![]() 处切线
处切线![]() 交
交![]() 于点
于点![]() ,下列结论正确的是 .(写出所有正确结论的序号)
,下列结论正确的是 .(写出所有正确结论的序号)
①若![]() ,则弧
,则弧![]() 的长为
的长为![]() ; ②若
; ②若![]() ,则
,则![]() 平分
平分![]() ;
;
③若![]() ,则
,则![]() ; ④无论点
; ④无论点![]() 在弧
在弧![]() 上的位置如何变化,
上的位置如何变化,![]() 为定值.
为定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中:①线段是轴对称图形,②成轴对称的两个图形对称点的连线互相平行,③等腰三角形的角平分线就是底边的垂直平分线,④已知两腰就能确定等腰三角形的形状和大小,正确的有( ) .
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各数中,正确的角度互化是( )
A.63.5°=63°50′B.23°12′36″=23.48°
C.18°18′18″=18.33°D.22.25°=22°15′
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】位于张家界核心景区的贺龙铜像,是我国近百年来最大的铜像.铜像由像体AD和底座CD两部分组成.如图,在Rt△ABC中,∠ABC=70.5°,在Rt△DBC中,∠DBC=45°,且CD=2.3米,求像体AD的高度(最后结果精确到0.1米,参考数据:sin70.5°≈0.943,cos70.5°≈0.334,tan70.5°≈2.824)
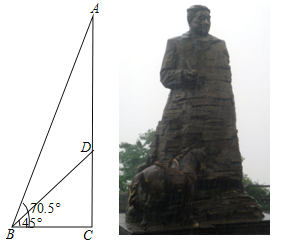
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数 ![]() 与x轴、y轴分别相交于点A和点B,直线
与x轴、y轴分别相交于点A和点B,直线 ![]() 经过点C(1,0)且与线段AB交于点P,并把△ABO分成两部分.
经过点C(1,0)且与线段AB交于点P,并把△ABO分成两部分.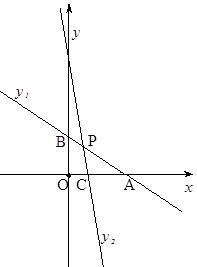
(1)求△ABO的面积;
(2)若△ABO被直线CP分成的两部分的面积相等,求点P的坐标及直线CP的函数表达式。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com