
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,分别过点B、C两点作过点A的直线的垂线,垂足为M、N.

(1)如图1,当M、N两点在直线BC的同侧时,求证:BM+CN=MN;
(2)如图2,当M、N两点在直线BC的两侧时,BM、CN、MN三条线段的数量关系并证明.
【答案】(1)见解析;(2)见解析.
【解析】
(1)由垂线的定义和角的互余关系得出∠AMB=∠CNA=90°,∠ABM=∠CAN,由AAS证明△ABM≌△CAN,得出对应边相等BM=AN,AM=CN,由AN+AM=MN,即可得出结论;
(2)由垂线的定义和角的互余关系得出∠AMB=∠CNA=90°,∠ABM=∠CAN,由AAS证明△ABM≌△CAN,得出对应边相等BM=AN,AM=CN,由AN+MN=AM,即可得出结论.
(1)证明:∵∠BAC=90°,
∴∠BAM+∠CAN=90°,
∵BM⊥l,BN⊥l,
∴∠AMB=∠CNA=90°,
∴∠BAM+∠ABM=90°,
∴∠ABM=∠CAN,
在△ABM和△CAN中,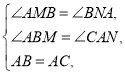
∴△ABM≌△CAN(AAS),
∴BM=AN,AM=CN,
∵AN+AM=MN,
∴BM+CN=MN;
(2)解:BM+MN=CN;理由如下:
∵∠BAC=90°,
∴∠BAM+∠CAN=90°,
∵BM⊥l,BN⊥l,
∴∠AMB=∠BNA=90°,
∴∠BAM+∠ABM=90°,
∴∠ABM=∠CAN,
在△ABM和△CAN中,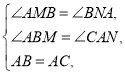 ,
,
∴△ABM≌△CAN(AAS),
∴BM=AN,AM=CN,
∵AN+MN=AM,
∴BM+MN=CN.


科目:初中数学 来源: 题型:
【题目】已知一圆形零件的标准直径是![]() ,超过规定直径长度的数量(毫米)记作正数,不足规定直径长度的数量(毫米)记作负数,检验员某次抽查了零件样品,检查的结果如下:
,超过规定直径长度的数量(毫米)记作正数,不足规定直径长度的数量(毫米)记作负数,检验员某次抽查了零件样品,检查的结果如下:
序号 |
|
|
|
|
|
直径长度/ |
|
|
|
|
|
(1)试指出哪件样品的大小最符合要求?
(2)如果规定误差的绝对值在![]() 之内是正品.误差的绝对值在
之内是正品.误差的绝对值在![]() 之间是次品,误差的绝对值超过
之间是次品,误差的绝对值超过![]() 的是废品,那么上述五件样品中,哪些是正品,哪些是次品,哪些是废品?
的是废品,那么上述五件样品中,哪些是正品,哪些是次品,哪些是废品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】己知有理数![]() 在数轴上所对应的点分别是
在数轴上所对应的点分别是![]() 三点,且
三点,且![]() 满足:①多项式
满足:①多项式![]() 是关于
是关于![]() 的二次三项式:②
的二次三项式:②![]()
![]() 请在图1的数轴上描出
请在图1的数轴上描出![]() 三点,并直接写出
三点,并直接写出![]() 三数之间的大小关系(用“<”连接) ;
三数之间的大小关系(用“<”连接) ;
![]() 点
点![]() 为数轴上
为数轴上![]() 点右侧一点,且点
点右侧一点,且点![]() 到
到![]() 点的距离是到
点的距离是到![]() 点距离的
点距离的![]() 倍,求点
倍,求点![]() 在数轴上所对应的有理数;
在数轴上所对应的有理数;
![]() 点
点![]() 在数轴上以每秒
在数轴上以每秒![]() 个单位长度的速度向左运动,同时点
个单位长度的速度向左运动,同时点![]() 和点
和点![]() 在数轴上分别以每秒
在数轴上分别以每秒![]() 个单位长度和
个单位长度和![]() 个单位长度的速度向右运动(其中
个单位长度的速度向右运动(其中![]() ),若在整个运动的过程中,点
),若在整个运动的过程中,点![]() 到点
到点![]() 的距离与点
的距离与点![]() 到点
到点![]() 的距离差始终不变,求
的距离差始终不变,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC与△CDE都是等腰直角三角形,∠ACB=90°,∠DCE=90°,连结BE,AD,相交于点F.求证:
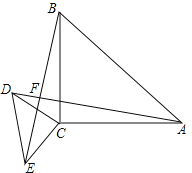
(1)AD=BE;
(2)AD⊥BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,BC⊥AF于点C,∠A+∠1=90°.
(1)求证:AB∥DE;
(2)如图2,点P从点A出发,沿线段AF运动到点F停止,连接PB,PE.则∠ABP,∠DEP,∠BPE三个角之间具有怎样的数量关系(不考虑点P与点A,D,C重合的情况)?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知用2辆A型车和1辆B型车载满货物一次可运货物10吨;用1辆A型车和2辆B型车载满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都载满货物.根据以上信息,解答下列问题:
(1)用1辆A型车和1辆B型车都载满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案.若A型车每辆需租金100元/次,B型车每辆需租金120元/次.请选出最省钱的租车方案,并求出最少租车费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB是⊙O的直径,AB=4,点F,C是⊙O上两点,连接AC,AF,OC,弦AC平分∠FAB,∠BOC=60°,过点C作CD⊥AF交AF的延长线于点D,垂足为点D.
(1)求扇形OBC的面积(结果保留π);
(2)求证:CD是⊙O的切线.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把2张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为m,宽为n)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示.阴影部分刚好能分割成两张形状大小不同的小长方形卡片(如图③),则分割后的两个阴影长方形的周长和是( )

A. 4mB. 2(m+n)C. 4nD. 4(m﹣n)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAC 的角平分线与 BC 的垂直平分线交于点 D,DE⊥AB, DF⊥AC,垂足分别为 E,F.若 AB=10,AC=8,求 BE 长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com