
【题目】骑自相车旅行越来越受到人们的喜爱,顺风车行经营的A型车2016年4月份销售总额为3.2万元,今年经过改造升级后A型车每辆销售比去年增加400元,若今年4月份与去年4月份卖出的A型车数量相同,则今年4月份A型车销售总额将比去年4月份销售总额增加25%.
(1)求今年4月份A型车每辆销售价多少元(用列方程的方法解答);
(2)该车行计划5月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多? A、B两种型号车的进货和销售价格如表:
A型车 | B型车 | |
进货价格(元/辆) | 1100 | 1400 |
销售价格(元/辆) | 今年的销售价格 | 2400 |
【答案】
(1)解:设去年A型车每辆x元,那么今年每辆(x+400)元,根据题意得:
![]() =
= ![]() ,
,
解得:x=1600,
经检验,x=1600是方程的解.
答:今年A型车每辆2000元
(2)解:设今年5月份进A型车m辆,则B型车(50﹣m)辆,获得的总利润为y元,
根据题意得:50﹣m≤2m
解得:m≥16 ![]() ,
,
∵y=(2000﹣1100)m+(2400﹣1400)(50﹣m)=﹣100m+50000,
∴y随m 的增大而减小,
∴当m=17时,可以获得最大利润.
答:进货方案是A型车17辆,B型车33辆
【解析】(1)设去年A型车每辆x元,那么今年每辆(x+400)元,根据今年4月份与去年4月份卖出的A型车数量相同,列方程求解即可;(2)设今年5月份进A型车m辆,则B型车(50﹣m)辆,获得的总利润为y元,先求出m的范围,构建一次函数,利用函数性质解决问题.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】作图题:
(1)如图,在平面内有不共线的3个点A,B,C.
(a)作直线AB,射线AC,线段BC;
(b)延长BC到点D,使CD=BC,连接AD;
(c)作线段AB的中点E,连接CE;
(d)测量线段CE和AD的长度,直接写出二者之间的数量关系_______.

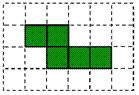
(2) 有5个大小一样的正方形制成如图所示的拼接图形(阴影部分),请你在图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.
注意:只需添加一个符合要求的正方形,并用阴影表示.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
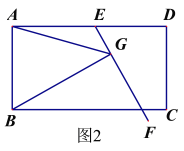
问题:如图1,在平行四边形ABCD中,E是AD上一点,AE=AB,∠EAB=60°,过点E作直线EF,在EF上取一点G,使得∠EGB=∠EAB,连接AG.
求证:EG =AG+BG.
小明同学的思路是:作∠GAH=∠EAB交GE于点H,构造全等三角形,经过推理解决问题.
参考小明同学的思路,探究并解决下列问题:
(1)完成上面问题中的证明;
(2)如果将原问题中的“∠EAB=60°”改为“∠EAB=90°”,原问题中的其它条件不变(如图2),请探究线段EG、AG、BG之间的数量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图四边形ABCD中,AD=DC,∠DAB=∠ACB=90°,过点D作DF⊥AC,垂足为F.DF与AB相交于E.设AB=15,BC=9,P是射线DF上的动点.当△BCP的周长最小时,DP的长为 . 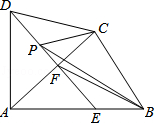
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场服装部为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励.为了确定一个适当的月销售目标,商场服装部统计了每个营业员在某月的销售额(单位:万元),数据如下:
17 18 16 13 24 15 28 26 18 19
22 17 16 19 32 30 16 14 15 26
15 32 23 17 15 15 28 28 16 19
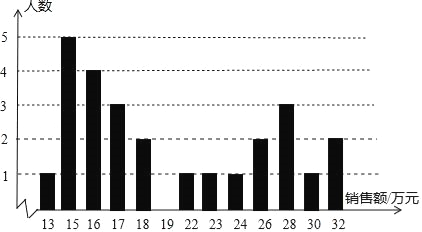
(1)补全条形图;
(2)月销售额为 的人数最多;
(3)如果想让一半左右的营业员都能达到销售目标,月销售目标定为多少合适?
A.15万元 B.16万元 C.18万元 D.19万元
(4)如果想确定一个较高的销售目标,你认为月销售目标定为多少合适?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD和正方形DEFG的顶点在y轴上,顶点D,F在x轴上,点C在DE边上,反比例函数y= ![]() (k≠0)的图象经过B,C和边EF的中点M,若S四边形ABCD=8,则正方形DEFG的面积是( )
(k≠0)的图象经过B,C和边EF的中点M,若S四边形ABCD=8,则正方形DEFG的面积是( )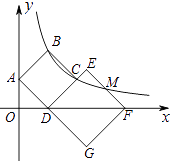
A.![]()
B.![]()
C.16
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C是直角,AB=6cm,∠ABC=60°,将△ABC以点B为中心顺时针旋转,使点C旋转到AB边延长线上的D处,则AC边扫过的图形众人阴影部分的面积是 . 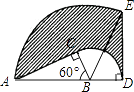
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,点E是边BC的中点,连接AE并延长,交DC的延长线于点F,连接AC,BF.
(1)求证:△ABE≌△FCE;
(2)当四边形ABFC是矩形时,当∠AEC=80°,求∠D的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一长方形休闲广场的四角都设计一块半径相同的四分之一圆的花坛,正中设计一个圆形喷水池,若四周圆形和中间圆形的半径均为![]() 米,广场长为
米,广场长为![]() 米,宽为
米,宽为![]() 米.
米.
(1)请列式表示广场空地的面积;
(2)若休闲广场的长为500米,宽为300米,圆形花坛的半径为20米,求广场空地的面积(计算结果保留![]() ).
).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com