
分析 首先把原方程化为一般形式,然后根据求根公式即可求得结果.
解答 解:原方程可化为:(a-c)x2+2bx+(a+c)=0,
当三角形是锐角三角形时,
∵a为最大边,
∴a-c≠0,
∵△=4b2-4a2+4c2,
∵a,b,c为△ABC的三边,
∴△>0,
∴x=$\frac{-2b±\sqrt{△}}{2(a-c)}$=$\frac{-2b±2\sqrt{{b}^{2}-{a}^{2}+{c}^{2}}}{2(a-c)}$=$\frac{-b±\sqrt{{b}^{2}-{a}^{2}+{c}^{2}}}{a-c}$,
∴x1=$\frac{-b+\sqrt{{b}^{2}-{a}^{2}+{c}^{2}}}{a-c}$,
x2=$\frac{-b-\sqrt{{b}^{2}-{a}^{2}+{c}^{2}}}{a-c}$,
当三角形是直角三角形时,
∵△=4b2-4a2+4c2=0,
∴x1=x2=$\frac{-b}{a-c}$;
当三角形是钝角三角形时,△<0,方程无实数根.
点评 本题考查了解一元二次方程,根的判别式,熟练掌握解一元二次方程的方法是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
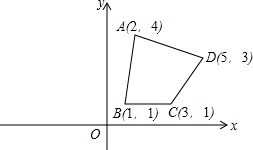 如图所示,四边形ABCD的顶点坐标分别为A(2,4)、B(1,1)、C(3,1)、D(5,3),请你补画出它关于y轴对称的图形A′B′C′D′,并写出顶点的坐标.
如图所示,四边形ABCD的顶点坐标分别为A(2,4)、B(1,1)、C(3,1)、D(5,3),请你补画出它关于y轴对称的图形A′B′C′D′,并写出顶点的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,长方形ABCD中,AD=8cm,CD=4cm.
如图,长方形ABCD中,AD=8cm,CD=4cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -15 | B. | 15 | C. | -$\frac{15}{2}$ | D. | $\frac{15}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 分数 | 70 | 80 | 90 | 100 |
| 人数 | 1 | 3 | x | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com