
 如图,长方形ABCD中,AD=8cm,CD=4cm.
如图,长方形ABCD中,AD=8cm,CD=4cm.分析 (1)设PD=x,则PA=8-x,若PA=PC,则PC=8-x,由矩形的性质和勾股定理得出方程x2+42=(8-x)2,解方程即可;
(2)先证出$\frac{AQ}{AP′}=\frac{P′D}{AP′}$,再由∠P′AQ=∠D=90°,得出△AP′Q∽△DCP′,得出对应角相等∠AP′Q=∠DCP′,由角的互余关系证出∠CP′Q=90°,即可得出QP′⊥P′C.
解答 解:(1)如图1所示: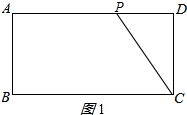
设PD=x,则PA=8-x,
若PA=PC,则PC=8-x,
∵四边形ABCD是矩形,
∴∠D=∠BAD=90°,
根据勾股定理得:PD2+CD2=PC2,
即x2+42=(8-x)2,
解得:x=3,
∴当点P在距离点D3cm处时,PA=PC;
(2)QP′⊥P′C;理由如下:如图2所示: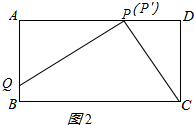
由(1)得:AP′=5,
∵$\frac{AQ}{AP′}=\frac{\frac{15}{4}}{5}$=$\frac{3}{4}$,$\frac{P′D}{AP′}=\frac{3}{4}$,
∴$\frac{AQ}{AP′}=\frac{P′D}{AP′}$,
又∵∠P′AQ=∠D=90°,
∴△AP′Q∽△DCP′,
∴∠AP′Q=∠DCP′,
∵∠CP′D+∠DCP′=90°,
∴∠CP′D+∠AP′Q=90°,
∴∠CP′Q=90°,
∴QP′⊥P′C.
点评 本题考查了矩形的性质、勾股定理、相似三角形的判定与性质;熟练掌握矩形的性质,并能进行推理论证与计算是解决问题的关键.


 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
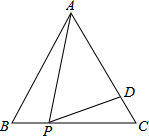 如图,在等边三角形ABC中,P为BC上一点,D为AC上一点,且∠APD=60°,BP=1,CD=$\frac{2}{3}$,则△ABC的边长为3.
如图,在等边三角形ABC中,P为BC上一点,D为AC上一点,且∠APD=60°,BP=1,CD=$\frac{2}{3}$,则△ABC的边长为3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
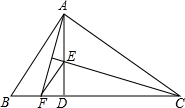 如图,已知在Rt△ABC中,∠BAC=90°,AD⊥BC于D,CE为∠ACB的平分线交AD于E,AF为∠BAD的平分线,交BC于F,求证:△ACE≌△FCE.
如图,已知在Rt△ABC中,∠BAC=90°,AD⊥BC于D,CE为∠ACB的平分线交AD于E,AF为∠BAD的平分线,交BC于F,求证:△ACE≌△FCE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
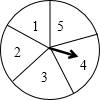 如图所示,转盘被等分成五个扇形,并在上面依次写上数字1、2、3、4、5,若自由转动转盘,当它停止转动时,指针指向奇数区域的概率是$\frac{3}{5}$.
如图所示,转盘被等分成五个扇形,并在上面依次写上数字1、2、3、4、5,若自由转动转盘,当它停止转动时,指针指向奇数区域的概率是$\frac{3}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com