
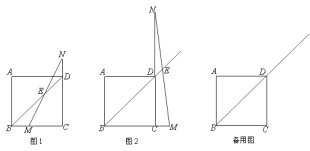
【题目】在正方形ABCD中,点M是射线BC上一点,点N是CD延长线上一点,且BM=DN.直线BD与MN相交于E.
(1)如图1,当点M在BC上时,求证:BD-2DE=![]() BM;
BM;
(2)如图2,当点M在BC延长线上时,BD、DE、BM之间满足的关系式是什么?;
(3)在(2)的条件下,连接BN交AD于点F,连接MF交BD于点G.若DE=![]() ,且AF:FD=1:2时,求线段DG的长.
,且AF:FD=1:2时,求线段DG的长.
【答案】(1)证明见试题解析;(2)BD+2DE=![]() BM;(3)
BM;(3)![]() .
.
【解析】
试题(1)过点M作MF⊥BC交BD于点F,推出FM=DN,根据AAS证△EFM和△EDN全等,推出DE=EF,根据正方形的性质和勾股定理求出即可;
(2)过点M作MF⊥BC交BD于点F,推出FM=DN,根据AAS证△EFM和△EDN全等,推出DE=EF,根据正方形的性质和勾股定理求出即可;
(3)根据已知求出CM的长,证△ABF∽△DNF,得出比例式,代入后求出CD长,求出FM长即可.
试题解析:(1)过点M作MF⊥BC交BD于点F,∵四边形ABCD是正方形,∴∠C=90°,∴FM∥CD,∴∠NDE=∠MFE,∴FM=BM,∵BM=DN,∴FM=DN,在△EFM和△EDN中,∵∠NDE=∠MFE,∠NED=∠MEF,DN=FM,∴△EFM≌△EDN,∴EF=ED,∴BD﹣2DE=BF,根据勾股定理得:BF=![]() BM,即BD﹣2DE=
BM,即BD﹣2DE=![]() BM;
BM;
(2)过点M作MF⊥BC交BD于点F,与(1)证法类似:BD+2DE=BF=![]() BM,故答案为:BD+2DE=
BM,故答案为:BD+2DE=![]() BM;
BM;
(3)由(2)知,BD+2DE=![]() BM,BD=
BM,BD=![]() BC,∵DE=
BC,∵DE=![]() ,∴CM=2,∵AB∥CD,∴△ABF∽△DNF,∴AF:FD=AB:ND,∵AF:FD=1:2,∴AB:ND=1:2,∴CD:ND=1:2,CD:(CD+2)=1:2,∴CD=2,∴FD=
,∴CM=2,∵AB∥CD,∴△ABF∽△DNF,∴AF:FD=AB:ND,∵AF:FD=1:2,∴AB:ND=1:2,∴CD:ND=1:2,CD:(CD+2)=1:2,∴CD=2,∴FD=![]() ,∴FD:BM=1:3,∴DG:BG=1:3,∴DG=
,∴FD:BM=1:3,∴DG:BG=1:3,∴DG=![]() .
.
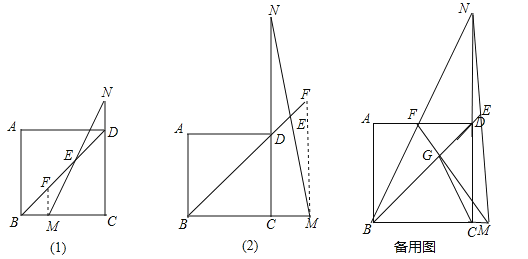


科目:初中数学 来源: 题型:
【题目】由于国家重点扶持节能环保产业,某种节能产品的销售市场逐渐回暖,某经销商销售这种产品,年初与生产厂家签订了一份进货合同,约定一年内进价为0.1万元/台.若一年内该产品的售价y(万元/台)与月份x(1≤x≤12且为整数)满足关系式:y=![]() ,一年后,发现这一年来实际每月的销售量p(台)与月份x之间存在如图所示的变化趋势.
,一年后,发现这一年来实际每月的销售量p(台)与月份x之间存在如图所示的变化趋势.
(1)求实际每月的销售量p(台)与月份x之间的函数表达式;
(2)全年中哪个月份的实际销售利润w最高,最高为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
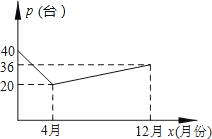
【题目】(1)观察发现:如图1,在Rt△ABC中,∠B=90°,点D在边AB上,过D作DE∥BC交AC于E,AB=5,AD=3,AE=4.填空:
①△ABC与△ADE是否相似?(直接回答) ;
②AC= ;DE= .
(2)拓展探究:将△ADE绕顶点A旋转到图2所示的位置,猜想△ADB与△AEC是否相似?若不相似,说明理由;若相似,请证明.
(3)迁移应用:将△ADE绕顶点A旋转到点B、D、E在同一条直线上时,直接写出线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是

A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
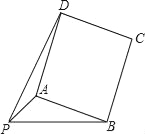
【题目】已知:PA=![]() ,PB=4,以AB为一边作正方形ABCD,使P、D两点落在直线AB的两侧.
,PB=4,以AB为一边作正方形ABCD,使P、D两点落在直线AB的两侧.
(1)如图,当∠APB=45°时,求AB及PD的长;
(2)当∠APB变化,且其它条件不变时,求PD的最大值,及相应∠APB的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,邻边不等的矩形花圃ABCD,它的一边AD利用已有的围墙,另外三边所围的栅栏的总长度是6m.若矩形的面积为4m2,求AB的长度。(可利用的围墙长度不超过3m)

查看答案和解析>>
科目:初中数学 来源: 题型:
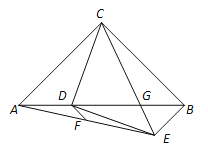
【题目】如图,在Rt△ABC中,AC=BC,∠ACB=90°,点D为边AB上一点,CD绕点D顺时针旋转90°至DE,CE交AB于点G.已知AD=8,BG=6,点F是AE的中点,连接DF,求线段DF的长___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解2014届某校男生报考泉州市中考体育测试项目的意向,某校课题研究小组从毕业年段各班男生随机抽取若干人组成调查样本,根据收集整理到的数据绘制成以下不完全统计图.根据以上信息,解答下列问题:
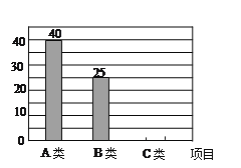

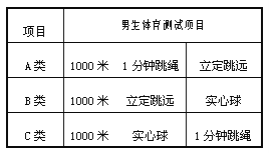
(1)该小组采用的调查方式是____________,被调查的样本容量是_______;
(2)请补充完整图中的条形统计图和扇形统计图(请标上百分率)(百分率精确到1%);
(3)该校共有600名初三男生,请估计报考A类的男生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com