
【题目】如图,⊙O的半径为3,A,P两点在⊙O上,点B在⊙O内,tan∠APB=![]() ,AB⊥AP.如果OB⊥OP,那么OB的长为_____.
,AB⊥AP.如果OB⊥OP,那么OB的长为_____.
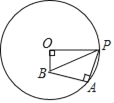
【答案】1
【解析】
如图,连接OA,作AM⊥OB交OB的延长线于M,作PN⊥MA交MA的延长线于N.则四边形POMN是矩形.想办法求出OM、BM即可解决问题;
解:如图,连接OA,作AM⊥OB交OB的延长线于M,作PN⊥MA交MA的延长线于N.则四边形POMN是矩形.
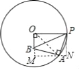
∵∠POB=∠PAB=90°,
∴P、O、B、A四点共圆,
∴∠AOB=∠APB,
∴tan∠AOM=tan∠APB=![]() =
=![]() ,设AM=4k,OM=3k,
,设AM=4k,OM=3k,
在Rt△OMA中,(4k)2+(3k)2=32,
解得k=![]() (负根已经舍弃),
(负根已经舍弃),
∴AM=![]() ,OM=
,OM=![]() ,AN=MN﹣AM=
,AN=MN﹣AM=![]() ,
,
∵∠MAB+∠ABM=90°,∠MAB+∠PAN=90°,
∴∠ABM=∠PAN,∵∠AMB=∠PNA=90°,
∴△AMB∽△PNA,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴BM=![]() ,
,
∴OB=OM﹣BM=1.
故答案为1


科目:初中数学 来源: 题型:
【题目】在“植树节”期间,小王、小李两人想通过摸球的方式来决定谁去参加学校植树活动,规则如下:在两个盒子内分别装入标有数字1,2,3,4的四个和标有数字1,2,3的三个完全相同的小球,分别从两个盒子中各摸出一个球,如果所摸出的球上的数字之和小于5,那么小王去,否则就是小李去.
(1)用树状图或列表法求出小王去的概率;
(2)小李说:“这种规则不公平”,你认同他的说法吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
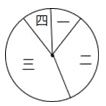
【题目】某校在践行“社会主义核心价值观”演讲比赛中,对名列前20名的选手的综合分数m进行分组统计,结果如表所示:

(1)求a的值;
(2)若用扇形图来描述,求分数在6≤m<7内所对应的扇形图的圆心角大小;
(3)将在第一组内的两名选手记为:A1、A2,在第四组内的两名选手记为:B1、B2,从第一组和第四组中随机选取2名选手进行调研座谈,求第一组至少有1名选手被选中的概率(用树状图或列表法列出所有可能结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年9月热播的专题片《辉煌中国﹣﹣圆梦工程》展示的中国桥、中国路等超级工程展现了中国现代化进程中的伟大成就,大家纷纷点赞“厉害了,我的国!”片中提到我国已成为拥有斜拉桥最多的国家,世界前十座斜拉桥中,中国占七座,其中苏通长江大桥(如图1所示)主桥的主跨长度在世界斜拉桥中排在前列.在图2的主桥示意图中,两座索塔及索塔两侧的斜拉索对称分布,大桥主跨BD的中点为E,最长的斜拉索CE长577m,记CE与大桥主梁所夹的锐角∠CED为α,那么用CE的长和α的三角函数表示主跨BD长的表达式应为BD=_____(m).

查看答案和解析>>
科目:初中数学 来源: 题型:
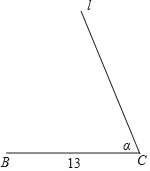
【题目】如图,线段BC长为13,以C为顶点,CB为一边的∠α满足cosα=![]() .锐角△ABC的顶点A落在∠α的另一边上,且满足sinA=
.锐角△ABC的顶点A落在∠α的另一边上,且满足sinA=![]() .求△ABC的高BD及AB边的长,并结合你的计算过程画出高BD及AB边.(图中提供的单位长度供补全图形使用)
.求△ABC的高BD及AB边的长,并结合你的计算过程画出高BD及AB边.(图中提供的单位长度供补全图形使用)
查看答案和解析>>
科目:初中数学 来源: 题型:
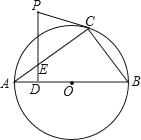
【题目】如图,△ABC内接于⊙O,AB是⊙O的直径.PC是⊙O的切线,C为切点,PD⊥AB于点D,交AC于点E.
(1)求证:∠PCE=∠PEC;
(2)若AB=10,ED=![]() ,sinA=
,sinA=![]() ,求PC的长.
,求PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
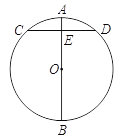
【题目】在我国古代数学著作《九章算术》中记载了这样一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现代语言表述为:如图,AB为⊙O的直径,弦CD⊥AB于点E,AE = 1寸,CD = 10寸,求直径AB的长.请你解答这个问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习解直角三角形以后,重庆八中数学兴趣小组测量了旗杆的高度.如图,某一时刻,旗杆AB的影子一部分落在平台上的影长BC为6米,落在斜坡上的影长CD为4米,AB⊥BC,同一时刻,光线与旗杆的夹角为37°,斜坡的坡角为30°,旗杆的高度AB约为( )米.(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75, ![]() ≈1.73)
≈1.73)
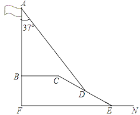
A. 10.61 B. 10.52 C. 9.87 D. 9.37
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,∠ADC的平分线与AB交于E,点F在DE的延长线上,∠BFE=90°,连接AF、CF,CF与AB交于G.有以下结论:
①AE=BC
②AF=CF
③BF2=FGFC
④EGAE=BGAB
其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com