
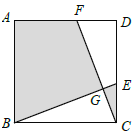
【题目】如图,在正方形![]() 中,
中,![]() ,点
,点![]() 分别在
分别在![]() 、
、![]() 上,
上,![]() ,
,![]() 相交于
相交于![]() . 若图中阴影部分的面积与正方形
. 若图中阴影部分的面积与正方形![]() 的面积之比为
的面积之比为![]() ,则
,则![]() 的周长为______.
的周长为______.
【答案】![]()
【解析】
根据阴影部分的面积与正方形ABCD的面积之比为2:3,得出阴影部分的面积为24,空白部分的面积为12,进而依据△BCG的面积以及勾股定理,得出BG+CG的长,进而得出其周长.
解:∵阴影部分的面积与正方形ABCD的面积之比为2:3,
∴阴影部分的面积为![]()
∴空白部分的面积为36-24=12,
由CE=DF,BC=CD,∠BCE=∠CDF=90°,可得△BCE≌△CDF,
∴△BCG的面积与四边形DEGF的面积相等,均为![]() ,
,
∠CBE=∠DCF,
∵∠DCF+∠BCG=90°,
∴∠CBG+∠BCG=90°,即∠BGC=90°,
设BG=a,CG=b,则![]() ,
,
又∵a2+b2=62,
∴a2+2ab+b2=36+24=60,
即(a+b)2=60,
∴a+b=![]() ,即BG+CG=
,即BG+CG=![]() ,
,
∴△BCG的周长=![]()
故答案为:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(本题10分)如图,AB是⊙O的直径,BC是⊙O的弦,半径OD⊥BC,垂足为E,若BC=![]() ,DE=3.
,DE=3.

求:(1)⊙O的半径;(2)弦AC的长;(3)阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
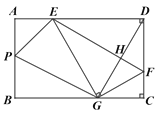
【题目】如图,在矩形ABCD中,点E,F分别在边AD,DC上,AB=6,DF=4,将矩形沿直线EF折叠,点D恰好落在BC边上的点G处,连接DG交EF于点H.
(1)求DE的长度.
(2)求![]() 的值.
的值.
(3)若AB边上有且只存在2个点P,使△APE与△BPG相似,请直接写出边AD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
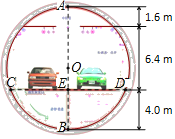
【题目】如图,是一张盾构隧道断面结构图.隧道内部为以O为圆心,AB为直径的圆.隧道内部共分为三层,上层为排烟道,中间为行车隧道,下层为服务层.点A到顶棚的距离为1.6m,顶棚到路面的距离是6.4m,点B到路面的距离为4.0m.请求出路面CD的宽度.(精确到0.1m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC的中点,E是AD的中点,过点A作AF∥BC,AF与CE的延长线相交于点F,连接BF.

(1)求证:四边形AFBD是平行四边形;
(2)将下列命题填写完整,并使命题成立(图中不再添加其它的点和线):
①当△ABC满足条件AB=AC时,四边形AFBD是 形;
② 当△ABC满足条件 时,四边形AFBD是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】石狮泰禾某童装专卖店在销售中发现,一款童装每件进价为80元,销售价为120元时,每天可售出20件,为了迎接“十一”国庆节,商店决定采取适当的降价措施,以扩大销售量,增加利润,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件.
(1)设每件童装降价x元时,每天可销售______ 件,每件盈利______ 元;(用x的代数式表示)
(2)每件童装降价多少元时,平均每天赢利1200元.
(3)要想平均每天赢利2000元,可能吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正面分别标有数字![]() ,
,![]() ,
,![]() ,背面花色相同的三张卡片洗匀后,背面朝上放在桌面上.
,背面花色相同的三张卡片洗匀后,背面朝上放在桌面上.
(1)随机地抽取一张,求这张卡片上的数字为偶数的概率;
(2)随机地抽取一张作为个位上的数字(不放回),再抽取一张作为十位上的数字,能组成哪些两位数恰好为“![]() ”的概率是多少?
”的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com