
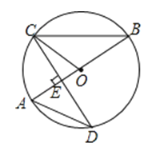
【题目】如图,![]() 是圆
是圆![]() 的直径.
的直径.![]() 是圆
是圆![]() 的一条弦.且
的一条弦.且![]() 于点
于点![]() .
.
(1)若![]() ,求
,求![]() 的大小;
的大小;
(2)若![]() .
.![]() ,求弧
,求弧![]() 的长.
的长.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)首先求出∠ADE的度数,再根据圆周角定理求出∠AOC的度数,根据直角三角形的两个锐角互余求出∠OCE的度数;
(2)根据三角函数可求∠A=60°,可得∠BOD=120°,由弦CD与直径AB垂直,利用垂径定理得到E为CD的中点,求出DE、CE的长,在直角三角形OCE中,设圆的半径OC=r,OE=OA-AE,表示出OE,利用勾股定理列出关于r的方程,求出方程的解,即可得到圆的半径r的值,根据弧长的公式即可得到结论.
(1)∵![]() ,
,
∴![]()
∵![]() ,
,
∴![]() .
.
∴![]() ,
,
∴![]() ;
;
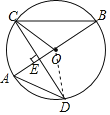
(2)解:∵![]() 是圆
是圆![]() 的直径,且
的直径,且![]() 于点
于点![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
设圆![]() 的半径为
的半径为![]() ,则
,则![]() ,
,![]() ,
,
所以![]() ,
,
解得:![]() .∴圆
.∴圆![]() 的半径为4,
的半径为4,
连接![]() ,
,
∴弧![]() 的长
的长![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】(6分)某海域有A,B两个港口,B港口在A港口北偏西30°方向上,距A港口60海里,有一艘船从A港口出发,沿东北方向行驶一段距离后,到达位于B港口南偏东75°方向的C处,求该船与B港口之间的距离即CB的长(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
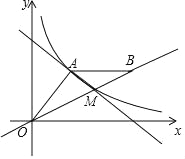
【题目】如图,A(8,6)是反比例函数y=![]() (x>0)在第一象限图象上一点,连接OA,过A作AB∥x轴,且AB=OA(B在A右侧),直线OB交反比例函数y=
(x>0)在第一象限图象上一点,连接OA,过A作AB∥x轴,且AB=OA(B在A右侧),直线OB交反比例函数y=![]() 的图象于点M
的图象于点M
(1)求反比例函数y=![]() 的表达式;
的表达式;
(2)求点M的坐标;
(3)设直线AM关系式为y=nx+b,观察图象,请直接写出不等式nx+b﹣![]() ≤0的解集.
≤0的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市举行“传承好家风”征文比赛,已知每篇参赛征文成绩记m分(60≤m≤100),组委会从1000篇征文中随机抽取了部分参赛征文,统计了它们的成绩,并绘制了如图不完整的两幅统计图表.
征文比赛成绩频数分布表
分数段 | 频数 | 频率 |
60≤m<70 | 38 | 0.38 |
70≤m<80 | a | 0.32 |
80≤m<90 | b | c |
90≤m≤100 | 10 | 0.1 |
合计 | 1 |
请根据以上信息,解决下列问题:
(1)征文比赛成绩频数分布表中c的值是_____;
(2)补全征文比赛成绩频数分布直方图;
(3)若80分以上(含80分)的征文将被评为一等奖,试估计全市获得一等奖征文的篇数.

查看答案和解析>>
科目:初中数学 来源: 题型:
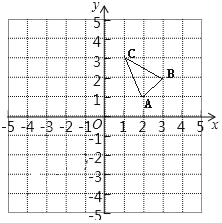
【题目】在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上,请解答下列问题:
(1)作出△ABC向左平移4个单位长度后得到的△A1B1C1,并写出点C1的坐标;
(2)将△A1B1C1绕原点O逆时针旋转90°得到△A2B2C2,请画出旋转后的△A2B2C2,并写出点C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)“2015扬州鉴真国际半程马拉松”的赛事共有三项:A、“半程马拉松”、B、“10公里”、C、“迷你马拉松”。小明和小刚参加了该项赛事的志愿者服务工作,组委会随机将志愿者分配到三个项目组
(1)小明被分配到“迷你马拉松”项目组的概率为
(2)求小明和小刚被分配到不同项目组的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】感知:如图1,AD平分∠BAC.∠B+∠C=180°,∠B=90°,易知:DB=DC.
探究:如图2,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°,求证:DB=DC.
应用:如图3,四边形ABCD中,∠B=45°,∠C=135°,DB=DC=a,则AB﹣AC= (用含a的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中装有2个红球和1个白球这些球除颜色外都相同.
(1)小明认为,搅匀后从中任意摸出一个球,不是白球就是红球,因此摸出白球和红球是等可能的你同意吗?为什么.
(2)搅匀后从中一次摸出两个球,请通过列表或树状图求两个球是一红一白的概率;
(3)在这只袋中再放入若干个白球,搅匀后从中任意摸出一个球,要使摸出白球的概率为![]() ,应再放入多少个白球?
,应再放入多少个白球?
查看答案和解析>>
科目:初中数学 来源: 题型:
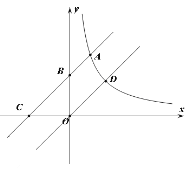
【题目】直线y=kx与反比例函数y=![]() (x>0)的图象相交点D(
(x>0)的图象相交点D(![]() ,m),将直线y=kx向上平移b个单位长度与反比例函数的图象交于点A,与y轴交于点B,与x轴交于点C,且
,m),将直线y=kx向上平移b个单位长度与反比例函数的图象交于点A,与y轴交于点B,与x轴交于点C,且![]() ,求平移后的直线的表达式.
,求平移后的直线的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com