【题目】如图，抛物线
与x轴交与A(1,0),B(- 3，0)两点
（1）求该抛物线的解析式；
（2）设（1）中的抛物线交y轴与C点，在该抛物线的对称轴上是否存在点Q，使得△QAC的周长最小？若存在，求出Q点的坐标；若不存在，请说明理由.
【答案】（1）
；（2）Q（-1，2）.
【解析】试题分析：（1）把A（1,0）B（-3，0）代入
然后解方程组即可；（2）因为线段AC的长固定不变，所以当AQ+CQ的长最小时△QAC的周长最小，根据轴对称的性质可知直线BC与对称轴的交点即为Q点，用待定系数法求直线BC解析式，把对称轴x=-1代入即可.
试题解析：解（1）把A（1,0）B（-3，0）代入到
3分
∴抛物线的解析式为y=-x2-2x+3 5分
（2）存在。 6分
过B、C作直线BC与对称轴x=-1的交点就是Q点，
设直线BC解析式为y=kx+b，把B（-3,0）C（0,3）代入到
令XQ="-1" 得YQ=2 ∴Q（-1，2） 10分
科目：初中数学 来源： 题型：
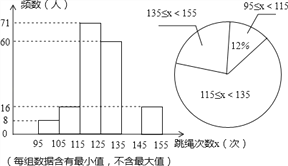
【题目】在我市开展的“阳光体育”跳绳活动中，为了了解中学生跳绳活动的开展情况，随机抽查了全市八年级部分同学1分钟跳绳的次数，将抽查结果进行统计，并绘制两个不完整的统计图．请根据图中提供的信息，解答下列问题：
（1）本次共抽查了多少名学生？
（2）请补全频数分布直方图空缺部分，直接写出扇形统计图中跳绳次数范围135≤x≤155所在扇形的圆心角度数．
（3）若本次抽查中，跳绳次数在125次以上（含125次）为优秀，请你估计全市8000名八年级学生中有多少名学生的成绩为优秀？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，在△ABC中，∠A=36°，AB=AC，∠ABC的平分线BE交AC于E．
（1）求证：AE=BC；
（2）如图（2），过点E作EF∥BC交AB于F，将△AEF绕点A逆时针旋转角α（0°＜α＜144°）得到△AE′F′，连结CE′，BF′，求证：CE′=BF′；
（3）在（2）的旋转过程中是否存在CE′∥AB？若存在，求出相应的旋转角α；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，Rt△AOB 中，∠AOB＝90°，OA＝3，OB＝4，将△AOB 沿 x 轴依次以三角形三个顶点为旋转中心顺时针旋转，分别得图②，图③，…，则旋转到图⑩时直角顶点的坐标是（ ）
A.（28，4）B.（36，0）C.（39，0）D.（
,
）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，抛物线
与x轴交于点A、B，与y轴交于点C，点O为坐标原点，点D为抛物线顶点，点E在抛物线上，点F在x轴上，四边形OCEF为矩形，且OF=2，EF=3
（1）求抛物线所对应的函数解析式；
（2）求ΔABC的面积。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在半径为27m的广场中央，点O的上空安装了一个照明光源S，S射向地面的光束呈圆锥形，其轴截面SAB的顶角为120°（如图），求光源离地面的垂直高度SO．（精确到0.1m；
=1.44，
=1.732，
=2.236，以上数据供参考）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下图是某汽车行驶的路程
与时间
（分钟）的函数关系图.
观察图中所提供的信息，解答下列问题：
（1）汽车在前
分钟内的平均速度是 .
（2）汽车在中途停了多长时间？
（3）当
时，求与的函数关系式
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
