
ЁОЬтФПЁПЮвУЧЖЈвхЃКСНИіЖўДЮЯюЯЕЪ§жЎКЭЮЊ1ЃЌЖдГЦжсЯрЭЌЃЌЧвЭМЯѓгыyжсНЛЕувВЯрЭЌЕФЖўДЮКЏЪ§ЛЅЮЊгбКУЭЌжсЖўДЮКЏЪ§ЃЎР§ШчЃКyЃН2x2+4xЉ5ЕФгбКУЭЌжсЖўДЮКЏЪ§ЮЊyЃНЉx2Љ2xЉ5ЃЎ
ЃЈ1ЃЉЧыФуаДГіyЃН![]() x2+xЉ5ЕФгбКУЭЌжсЖўДЮКЏЪ§ЃЛ
x2+xЉ5ЕФгбКУЭЌжсЖўДЮКЏЪ§ЃЛ
ЃЈ2ЃЉШчЭМЃЌЖўДЮКЏЪ§L1ЃКyЃНax2Љ4ax+1гыЦфгбКУЭЌжсЖўДЮКЏЪ§L2ЖМгыyжсНЛгкЕуAЃЌЕуBЁЂCЗжБ№дкL1ЁЂL2ЩЯЃЌЕуBЃЌCЕФКсзјБъОљЮЊmЃЈ0ЃМmЃМ2ЃЉЫќУЧЙигкL1ЕФЖдГЦжсЕФЖдГЦЕуЗжБ№ЮЊBЁфЃЌCЁфЃЌСЌНгBBЁфЃЌBЁфCЁфЃЌCЁфCЃЌCBЃЎШєaЃН3ЃЌЧвЫФБпаЮBBЁфCЁфCЮЊе§ЗНаЮЃЌЧѓmЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉyЃН![]() x2+2xЉ5ЃЛЃЈ2ЃЉ
x2+2xЉ5ЃЛЃЈ2ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнгбКУЭЌжсЖўДЮКЏЪ§ЕФЖЈвхЧѓГіМДПЩЃЛ
ЃЈ2ЃЉЯШИљОнЖўДЮКЏЪ§L1ЕФНтЮіЪНЕУГіЦфгбКУЭЌжсЖўДЮКЏЪ§L2ЕФКЏЪ§НтЮіЪНЃЌДњШыaЃН3ЃЌРћгУЖўДЮКЏЪ§ЭМЯѓЩЯЕуЕФзјБъЬиеїПЩЕУГіЕуBЁЂCЁЂBЁфЁЂCЁфЕФзјБъЃЌНјЖјПЩЕУГіBCЁЂBBЁфЕФжЕЃЌгЩе§ЗНаЮЕФаджЪПЩЕУBCЃНBBЁфЃЌМДПЩЕУГіЙигкmЕФвЛдЊЖўДЮЗНГЬЃЌНтжЎШЁЦфДѓгк0аЁгк2ЕФжЕМДЕУНсЙћЃЎ
НтЃКЃЈ1ЃЉЁп![]() ЃЌ1ЁСЃЈ
ЃЌ1ЁСЃЈ![]() ЃЉЃН2ЃЌ
ЃЉЃН2ЃЌ
ЁрКЏЪ§yЃН![]() x2+xЉ5ЕФгбКУЭЌжсЖўДЮКЏЪ§ЮЊyЃН
x2+xЉ5ЕФгбКУЭЌжсЖўДЮКЏЪ§ЮЊyЃН![]() x2+2xЉ5ЃЎ
x2+2xЉ5ЃЎ
ЃЈ2ЃЉЖўДЮКЏЪ§L1ЃКyЃНax2Љ4ax+1ЕФЖдГЦжсЮЊжБЯпxЃНЉ![]() ЃН2ЃЌЦфгбКУЭЌжсЖўДЮКЏЪ§L2ЃКyЃНЃЈ1ЉaЃЉx2Љ4ЃЈ1ЉaЃЉx+1ЃЎ
ЃН2ЃЌЦфгбКУЭЌжсЖўДЮКЏЪ§L2ЃКyЃНЃЈ1ЉaЃЉx2Љ4ЃЈ1ЉaЃЉx+1ЃЎ
ЁпaЃН3ЃЌ
ЁрЖўДЮКЏЪ§L1ЃКyЃНax2Љ4ax+1ЃН3x2Љ12x+1ЃЌЖўДЮКЏЪ§L2ЃКyЃНЃЈ1ЉaЃЉx2Љ4ЃЈ1ЉaЃЉx+1ЃНЉ2x2+8x+1ЃЌ
ЁрЕуBЕФзјБъЮЊЃЈmЃЌ3m2Љ12m+1ЃЉЃЌЕуCЕФзјБъЮЊЃЈmЃЌЉ2m2+8m+1ЃЉЃЌ
ЁрЕуBЁфЕФзјБъЮЊЃЈ4ЉmЃЌ3m2Љ12m+1ЃЉЃЌЕуCЁфЕФзјБъЮЊЃЈ4ЉmЃЌЉ2m2+8m+1ЃЉЃЌ
ЁрBCЃНЉ2m2+8m+1ЉЃЈ3m2Љ12m+1ЃЉЃНЉ5m2+20mЃЌBBЁфЃН4ЉmЉmЃН4Љ2mЃЎ
ЁпЫФБпаЮBBЁфCЁфCЮЊе§ЗНаЮЃЌ
ЁрBCЃНBBЁфЃЌМДЉ5m2+20mЃН4Љ2mЃЌ
НтЕУЃКm1ЃН![]() ЃЌm2ЃН
ЃЌm2ЃН![]() ЃЈВЛКЯЬтвтЃЌЩсШЅЃЉЃЌ
ЃЈВЛКЯЬтвтЃЌЩсШЅЃЉЃЌ
ЁрmЕФжЕЮЊ![]() ЃЎ
ЃЎ


 Н№АцПЮЬУПЮЪБбЕСЗЯЕСаД№АИ
Н№АцПЮЬУПЮЪБбЕСЗЯЕСаД№АИ ЕЅдЊШЋФмСЗПМОэЯЕСаД№АИ
ЕЅдЊШЋФмСЗПМОэЯЕСаД№АИ аТЛЦИдБјЗЈУмОэЯЕСаД№АИ
аТЛЦИдБјЗЈУмОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
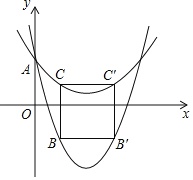
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌОиаЮOABCЕФСНБпOAЃЌOCЗжБ№дкxжсКЭyжсЩЯЃЌВЂЧвOAЃН5ЃЌOCЃН3ЃЎШєАбОиаЮOABCШЦзХЕуOФцЪБеыа§зЊЃЌЪЙЕуAЧЁКУТфдкBCБпЩЯЕФA1ДІЃЌдђЕуCЕФЖдгІЕуC1ЕФзјБъЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
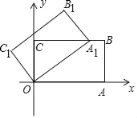
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDжаЃЌEЃЌFЃЌGЃЌHЗжБ№ЪЧБпABЁЂBCЁЂCDЁЂDAЕФжаЕуЃЎШєЫФБпаЮEFGHЮЊСтаЮЃЌдђЖдНЧЯпACЁЂBDгІТњзуЬѕМў__________ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
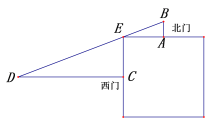
ЁОЬтФПЁПЮвЙњЙХДњЪ§бЇжјзїЁЖОХеТЫуЪѕЁЗжаМЧдиСЫвЛИіЮЪЬтЃКЁАНёгавиЗНВЛжЊДѓаЁЃЌИїПЊжаУХЃЌГіББУХШ§ЪЎВНгаФОЃЌГіЮїУХЦпАйЮхЪЎВНМћФОЃЌЮЪЃКвиЗНМИКЮЃПЁБ .ЦфДѓвтЪЧ:ШчЭМЃЌвЛзље§ЗНаЮГЧГиЃЌAЮЊББУХжаЕуЃЌДгЕуAЭље§ББЗНЯђзп30ВНЕНBГігавЛЪїФОЃЌCЮЊЮїУХжаЕуЃЌДгЕуCЭље§ЮїЗНЯђзп750ВНЕНDДІе§КУПДЕНBДІЕФЪїФОЃЌЧѓе§ЗНаЮГЧГиЕФБпГЄ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
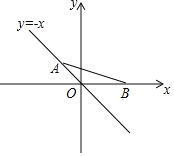
ЁОЬтФПЁПШчЭМЃЌЕуAЪЧжБЯпyЃНЉxЩЯЕФЖЏЕуЃЌЕуBЪЧxжсЩЯЕФЖЏЕуЃЌШєABЃН2ЃЌдђЁїAOBУцЛ§ЕФзюДѓжЕЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌАбвЛеХГЄ![]() ЃЌПэ
ЃЌПэ![]() ЕФОиаЮгВжНАхЕФЫФжмИїМєШЅвЛИіЭЌбљДѓаЁЕФе§ЗНаЮЃЌдйелКЯГЩвЛИіЮоИЧЕФГЄЗНЬхКазгЃЈжНАхЕФКёЖШКіТдВЛМЦЃЉЃЎ
ЕФОиаЮгВжНАхЕФЫФжмИїМєШЅвЛИіЭЌбљДѓаЁЕФе§ЗНаЮЃЌдйелКЯГЩвЛИіЮоИЧЕФГЄЗНЬхКазгЃЈжНАхЕФКёЖШКіТдВЛМЦЃЉЃЎ
ЃЈ1ЃЉвЊЪЙГЄЗНЬхКазгЕФЕзУцЛ§ЮЊ![]() ЃЌЧѓМєШЅЕФе§ЗНаЮЕФБпГЄЃЛ
ЃЌЧѓМєШЅЕФе§ЗНаЮЕФБпГЄЃЛ
ЃЈ2ЃЉФуОѕЕУелКЯЖјГЩЕФГЄЗНЬхКазгЕФВрУцЛ§ЛсВЛЛсгаИќДѓЕФЧщПіЃПШчЙћгаЃЌЧыЧѓГіВрУцЛ§ЕФзюДѓжЕКЭДЫЪБМєШЅЕФе§ЗНаЮЕФБпГЄЃЛШчЙћУЛгаЃЌЧыФуЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкаЃдАЮФЛЏвеЪѕНкжаЃЌОХФъМЖвЛАрга1УћФаЩњКЭ2УћХЎЩњЛёЕУУРЪѕНБЃЌСэга2УћФаЩњКЭ2УћХЎЩњЛёЕУвєРжНБЃЎ
ЃЈ1ЃЉДгЛёЕУУРЪѕНБКЭвєРжНБЕФ7УћбЇЩњжабЁШЁ1УћВЮМгАфНБДѓЛсЃЌЧѓИеКУЪЧФаЩњЕФИХТЪЃЛ
ЃЈ2ЃЉЗжБ№ДгЛёЕУУРЪѕНБЁЂвєРжНБЕФбЇЩњжаИїбЁШЁ1УћВЮМгАфНБДѓЛсЃЌгУСаБэЛђЪїзДЭМЧѓИеКУЪЧвЛФаЩњвЛХЎЩњЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЙигкxЕФвЛдЊЖўДЮЗНГЬЃЈm+1ЃЉx2ЉЃЈm+3ЃЉx+2ЃН0ЃЎ
ЃЈ1ЃЉжЄУїЃКЕБmЁйЉ1ЪБЃЌЗНГЬзмгаЪЕЪ§ИљЃЛ
ЃЈ2ЃЉmЮЊКЮећЪ§ЪБЃЌЗНГЬгаСНИіВЛЯрЕШЕФе§ећЪ§ИљЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
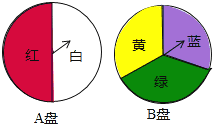
ЁОЬтФПЁПаЁгБЮЊАрМЖСЊЛЖЛсЩшМЦСЫвЛИіЁАХфзЯЩЋЁБгЮЯЗЃКЯТУцЪЧСНИіПЩвдздгЩзЊЖЏЕФзЊХЬЃЌУПИізЊХЬБЛЗж ГЩЯрЕШЕФМИИіЩШаЮЃЎгЮЯЗЙцдђЪЧЃКгЮЯЗепЭЌЪБзЊЖЏСНИізЊХЬЃЌШчЙћзЊХЬ A зЊГіСЫКьЩЋЃЌзЊХЬ B зЊГі СЫРЖЩЋЃЌФЧУДХфГЩСЫзЯЩЋЃЎ
ЃЈ1ЃЉРћгУЪїзДЭМЛђСаБэЕФЗНЗЈМЦЫуХфГЩзЯЩЋЕФИХТЪЃЎ
ЃЈ2ЃЉаЁКьКЭаЁССВЮМгетИігЮЯЗЃЌВЂдМЖЈХфГЩзЯЩЋаЁКьгЎЃЌСНИізЊХЬзЊГіЭЌжжбеЩЋЃЌаЁССгЎЃЎетИідМЖЈЖдЫЋЗНЙЋЦНТ№ЃПЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com