
【题目】如图,点A是直线y=﹣x上的动点,点B是x轴上的动点,若AB=2,则△AOB面积的最大值为_____.
【答案】![]() +1
+1
【解析】
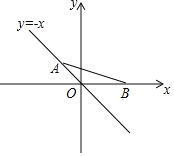
如图,作△AOB的外接圆⊙C,连接CB,CA,CO,过C作CD⊥AB于D,则CA=CB,连接OD,则OD≤OC+CD,依据当O,C,D在同一直线上时,OD的最大值为OC+CD,即可得到△AOB的面积最大值.
解:如图所示,作△AOB的外接圆⊙C,连接CB,CA,CO,过C作CD⊥AB于D,则CA=CB,
由题意可得∠AOB=45°,∴∠ACB=90°,
∴CD=![]() AB=1,AC=BC=
AB=1,AC=BC=![]() =CO,
=CO,
连接OD,则OD≤OC+CD,
∴当O,C,D在同一直线上时,OD的最大值为OC+CD=![]() +1,此时OD⊥AB,
+1,此时OD⊥AB,
∴△AOB的面积最大值为![]() AB×OD=
AB×OD=![]() ×2(
×2(![]() +1)=
+1)=![]() +1,
+1,
当点A在第二象限内,点B在x轴正半轴上时,同理可得,△AOB面积的最大值为![]() ﹣1(舍去).
﹣1(舍去).
故答案为:![]() +1.
+1.


科目:初中数学 来源: 题型:
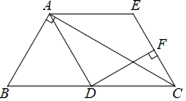
【题目】如图,在△ABC中,∠BAC=90°,点D是BC中点,AE∥BC,CE∥AD.
(1)求证:四边形ADCE是菱形;
(2)过点D作DF⊥CE于点F,∠B=60°,AB=6,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D为AC上一点,且CD=CB,以BC为直径作☉O,交BD于点E,连接CE,过D作DF![]() AB于点F,∠BCD=2∠ABD.
AB于点F,∠BCD=2∠ABD.
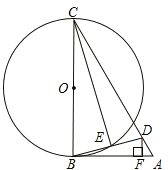
(1)求证:AB是☉O的切线;
(2)若∠A=60°,DF=![]() ,求☉O的直径BC的长。
,求☉O的直径BC的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阳光市场某个体商户购进某种电子产品,每个进价50元.调查发现,当售价为80元时,平均一周可卖出160个,而当每售价每降低2元时,平均一周可多卖出20个.若设每个电子产品降价x元,
(1)根据题意,填表:
进价(元) | 售价(元) | 每件利润(元) | 销量(个) | 总利润(元) | |
降价前 | 50 | 80 | 30 | 160 |
|
降价后 | 50 | ________ | ________ | ________ | ________ |
(2)若商户计划每周盈利5200元,且尽量减少库存,则每个电子产品应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:两个二次项系数之和为1,对称轴相同,且图象与y轴交点也相同的二次函数互为友好同轴二次函数.例如:y=2x2+4x﹣5的友好同轴二次函数为y=﹣x2﹣2x﹣5.
(1)请你写出y=![]() x2+x﹣5的友好同轴二次函数;
x2+x﹣5的友好同轴二次函数;
(2)如图,二次函数L1:y=ax2﹣4ax+1与其友好同轴二次函数L2都与y轴交于点A,点B、C分别在L1、L2上,点B,C的横坐标均为m(0<m<2)它们关于L1的对称轴的对称点分别为B′,C′,连接BB′,B′C′,C′C,CB.若a=3,且四边形BB′C′C为正方形,求m的值.
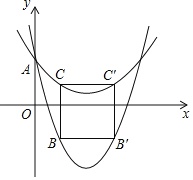
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=BC=6.点P在边AC上运动,过点P作PD⊥AB于点D,以AP、AD为邻边作PADE.设□PADE与△ABC重叠部分图形的面积为y,线段AP的长为x(0<x≤6).
(1)求线段PE的长(用含x的代数式表示).
(2)当点E落在边BC上时,求x的值.
(3)求y与x之间的函数关系式.
(4)直接写出点E到△ABC任意两边所在直线距离相等时x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=FM
(2)当AE=1时,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
= y2+8y+16 (第二步)
=(y+4)2 (第三步)
=(x2-4x+4)2 (第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式 B.平方差公式 C.两数和的完全平方公式 D.两数差的完全平方公式
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)
若不彻底,请直接写出因式分解的最后结果_________.
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com