
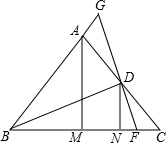
 如图,在△ABC中,AB=AC,BD、AM分别是∠ABC、∠BAC的平分线,DN⊥BC,GF⊥BD,求证:MN=$\frac{1}{4}$BF.
如图,在△ABC中,AB=AC,BD、AM分别是∠ABC、∠BAC的平分线,DN⊥BC,GF⊥BD,求证:MN=$\frac{1}{4}$BF. 分析 过D作DK∥BC交AB于K,推出△GBD≌△FBD,根据全等三角形的性质得到BG=BF,DG=DF,根据三角形的中位线的性质得到BK=KG,由直角三角形的性质得到DK=$\frac{1}{2}$BG,根据等腰三角形的性质得到DE=$\frac{1}{2}$DK,通过四边形EMND是矩形,得到DE=MN,等量代换得到结论.
解答 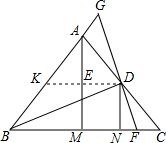 证明:过D 作DK∥BC交AB于K,
证明:过D 作DK∥BC交AB于K,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
在△GBD与△FBD中,
$\left\{\begin{array}{l}{∠BDG=∠FDB}\\{∠GBD=∠FBD}\\{BD=BD}\end{array}\right.$,
∴△GBD≌△FBD,
∴BG=BF,DG=DF,
∵DK∥BC,
∴BK=KG,
∵BD⊥GF,
∴DK=$\frac{1}{2}$BG,
∵AB=AC,AM平分∠BAC,
∴AM⊥BC,
∴AM⊥DK,
∴AK=AD,
∴DE=$\frac{1}{2}$DK,
∵∠DEM=∠EMN=∠DNM=90°,
∴四边形EMND是矩形,
∴DE=MN,
∴MN=$\frac{1}{2}$DK=$\frac{1}{2}×\frac{1}{2}$BG=$\frac{1}{4}$BF.
点评 本题考查了全等三角形的判定和性质,等腰三角形的性质,矩形的判定和性质,三角形的中位线的性质,熟练掌握全等三角形的判定和性质是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
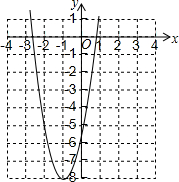 这是小明在阅读一本关于函数的课外读物时看到的一段文字:“由图象知,当x=-1时,二次函数y=ax2+6x-5的值最小”,你能写出a的值吗?
这是小明在阅读一本关于函数的课外读物时看到的一段文字:“由图象知,当x=-1时,二次函数y=ax2+6x-5的值最小”,你能写出a的值吗?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
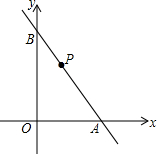 如图所示,已知直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于A,B两点,点P是线段AB上的一个动点,连结OP,把△ABO分成两个小三角形,分别是△AOP和△BOP,当AP的长为多少时,△AOP和△BOP中至少有一个是等腰三角形?
如图所示,已知直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于A,B两点,点P是线段AB上的一个动点,连结OP,把△ABO分成两个小三角形,分别是△AOP和△BOP,当AP的长为多少时,△AOP和△BOP中至少有一个是等腰三角形?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com