Question

【题目】如图，四边形ABCD中，∠DAB=∠ABC=90°，AB=BC，E是AB的中点，CE⊥BD．

（1）求证：BE=AD；

（2）求证：AC是线段ED的垂直平分线；

（3）△DBC是等腰三角形吗？并说明理由．

Answer 1

【答案】（1）见解析；（2）见解析；（3）△DBC是等腰三角形．见解析

【解析】

试题分析：（1）利用已知条件证明△DAB≌△EBC（ASA），根据全等三角形的对应边相等即可得到AD=BE；

（2）分别证明AD=AE，CE=CE，根据线段垂直平分线的逆定理即可解答；

（3）△DBC是等腰三角形，由△DAB≌△EBC，得到DB=EC，又有△AEC≌△ADC，得到EC=DC，所以DB=DC，即可解答．

解：（1）∵∠ABC=90°，

∴∠ABD+∠DBC=90°，

∵CE⊥BD，

∴∠BCE+∠DBC=90°，

∴∠ABD=∠BCE，

∵AD∥BC，

∴∠DAB=∠EBC，

在△DAB和△EBC中，

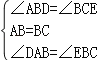
∴△DAB≌△EBC（ASA）

∴AD=BE

（2）∵E是AB的中点，即AE=BE，

∵BE=AD，

∴AE=AD，

∴点A在ED的垂直平分线上（到角两边相等的点在角的平分线上），

∵AB=BC，∠ABC=90°，

∴∠BAC=∠BCA=45°，

∵∠BAD=90°，

∴∠BAC=∠DAC=45°，

在△EAC和△DAC中，

，

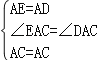∴△EAC≌△DAC（SAS）

∴CE=CD，

∴点C在ED的垂直平分线上

∴AC是线段ED的垂直平分线．

（3）△DBC是等腰三角形

∵△DAB≌△EBC，

∴DB=EC

∵△AEC≌△ADC，

∴EC=DC，

∴DB=DC，

∴△DBC是等腰三角形．