
����Ŀ����ͼ�٣���ABC�У�AB=AC����B����C��ƽ���߽���O�㣬��O����EF��BC��AB��AC��E��F.

(1)ͼ�����м�������������?����:EF��BE��CF֮���������Ĺ�ϵ.
(2)��ͼ��,��AB��AC�������������䣬ͼ�л��е�����������?����У��ֱ�ָ������.�ڵ�(1)����EF��BE��CF��Ĺ�ϵ��������?
(3)��ͼ�ۣ�����ABC�С�B��ƽ����BO�����������ƽ����CO����O����O����OE��BC��AB��E����AC��F.��ʱͼ�л��е�����������?EF��BE��CF��ϵ�����?˵���������.
���𰸡���1����AEF����OEB����OFC����OBC����ABC��5����EF=BE+FC����2���У���EOB����FOC�����ڣ���3���У�EF=BE-FC��
��������
��1����AB=AC���ɵá�ABC=��ACB������֪OB��OC�ֱ�ƽ�֡�ABC����ACB���ʡ�EBO=��OBC=��FCO=��OCB������EF��BC���ɵã���OEB=��OBC=��EBO����FOC=��FCO=��BCO���ɴ˿ɵó��ĵ����������У���AEF����OEB����OFC����OBC����ABC��
��֪�ˡ�EOB�͡�FOC�ǵ��������Σ���EO=BE��OF=FC����EF=BE+FC��
��2���ɣ�1����֤�����̿�֪����֤��OEB����OFC�ǵ��������εĹ����У���AB=AC������û�й�ϵ�������������������λ����������ԣ�1���еó���EF=BE+FC�Ľ����Գ�����
��3��˼·�루2����ͬ��ֻ������������EF=BE-FC��
�⣺��1��ͼ���ǵ��������ε��У���AEF����OEB����OFC����OBC����ABC��
EF��BE��FC�Ĺ�ϵ��EF=BE+FC���������£�
��AB=AC��
���ACB=��ABC����ABC�ǵ��������Σ�
��BO��CO�ֱ�ƽ�֡�ABC�͡�ACB��
���ABO=��OBC=![]() ��ABC����OCB=��ACO=
��ABC����OCB=��ACO=![]() ��ACB��
��ACB��
��EF��BC��
���EOB=��OBC����FOC=��OCB��
���ABO=��OBC=��EOB=��OCB=��FOC=��FCO��
���EOB����OBC����FOC���ǵ��������Σ�
��EF��BC��
���AEF=��ABC����AFE=��ACB��
���AEF=��AFE��
���AEF�ǵ��������Σ�
��OB��OCƽ�֡�ABC����ACB��
���ABO=��OBC����ACO=��OCB��
��EF��BC��
���EOB=��OBC=��EBO����FOC=��OCB=��FCO��
��EO=EB��FO=FC��
��EF=EO+OF=BE+CF��
��2����AB��ACʱ����EOB����FOC��Ϊ���������Σ���1���Ľ�����Ȼ������
��OB��OCƽ�֡�ABC����ACB��
���ABO=��OBC����ACO=��OCB��
��EF��BC��
���EOB=��OBC=��EBO����FOC=��OCB=��FCO��
��EO=EB��FO=FC��
��EF=EO+OF=BE+CF��
��3����EOB�͡�FOC���ǵ��������Σ�EF=BE-FC���������£�
ͬ��1����֤�á�EOB�ǵ��������Σ�
��EO��BC��
���FOC=��OCG��
��OCƽ�֡�ACG��
���ACO=��FOC=��OCG��
��FO=FC���ʡ�FOC�ǵ��������Σ�
��EF=EO-FO=BE-FC��


 ��һ������ĩ�ٷֳ�̾�ϵ�д�
��һ������ĩ�ٷֳ�̾�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��AB��CD�ཻ�ڵ�O������O����������OM��ON������AOM����CON��90��

(1)��OCƽ����AOM������AOD�Ķ�����
(2)����1��![]() ��BOC������AOC����MOD.
��BOC������AOC����MOD.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��������ABCD�У���E�ڱ�BC�ϣ���F��BA���ӳ����ϣ�BE=AF��CF��AE��CF���AD�ཻ�ڵ�G�� 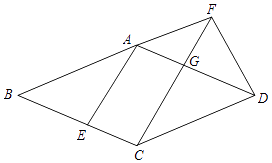
��֤��
��1��FD=CG��
��2��CG2=FGFC��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�κ���ͼ��x���ڵ�(��2,0)����y��Ľ��㵽ԭ��ľ���Ϊ5�����һ�κ�������ʽΪ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC����ABC=72�㣮

��1����ֱ�ߺ�Բ������ABC��ƽ����BD��AC�ڵ�D��������ͼ�ۼ�����Ҫ��д��������
��2���ڣ�1����������ABC��ƽ����BD�����BDC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ��ֱ������ϵ�У�OΪ����ABCD�ĶԳ����ģ���֪C��2��0����D��0����1����NΪ�߶�CD��һ�㣨����C��D�غϣ���
��1������CΪ���㣬�Ҿ�����D�������߽���ʽ��
��2����N����BD�ĶԳƵ�ΪN1 �� N����BC�ĶԳƵ�ΪN2 �� ��֤����N1BN2�ס�ABC��
��3����2����N1N2����Сֵ��
��4������N��y���ƽ���߽���1���е��������ڵ�P����QΪֱ��AB�ϵ�һ�����㣬�ҡ�PQA=��BAC����PQ��Сʱ��Q���꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ˮ�ν��IJ�����������ͼ��ʾ(ˮ�ε��ٶ�����ͬ��)����ôˮ�ĸ߶�h���������ʱ��t�仯�ģ���ѡ��ƥ���ʾ��ͼ��������
(A)����(������) (B)����(������)
(C)����(������) (D)����(������)

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ij�Ϊ15��Ϊ10����Ϊ20����B���C�ľ���Ϊ5��һֻ�������Ҫ���ų�����ı���ӵ�A������B����Ҫ���е���̾����ǣ� ��

A. 20 B. 25 C. 30 D. 32
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ijУ����֯ѧ����ѧ���ҳ������������ݽ������ʵ����Ϊ�˱��ڹ�����������Ա���������ͬһ�и����ϣ����ݱ���������������һ�������̻�Ʊ��6560Ԫ����������������̻�Ʊ������3120Ԫ��ѧ��Ʊ��������7.5�ۣ�һ���������ۣ�����֪ѧ���ҳ����ʦ������֮��Ϊ3��1����Ҧ��վ�����ݶ�վ�Ļ�Ʊ�۸������ʾ��
�������� | Ʊ�� | ||
�ϳ�վ | �³�վ | һ���� | ������ |
��Ҧ�� | ���ݶ� | 82��Ԫ�� | 48��Ԫ�� |
��1���μ����ʵ������ʦ���ҳ���ѧ�����ж����ˣ�
��2�����ڸ���ԭ��������Ʊ����ֻ����m�ţ�mС�ڲμ����ʵ���������������������һ������Ʊ���ڱ�֤ÿλ������Ա������λ����ǰ���£����������õĹ�Ʊ��������д�������Ʊ���ܷ��ã����̣�y��Ԫ�����ú�m�Ĵ���ʽ��ʾ����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com