
【题目】水滴进的玻璃容器如下图所示(水滴的速度是相同的),那么水的高度h是如何随着时间t变化的,请选择匹配的示意图与容器.
(A)——( ) (B)——( )
(C)——( ) (D)——( )

【答案】(A)——(3),(B)——(2),(C)——(4) , (D)——(1)
【解析】
根据各图中水高度与时间的关系进行判断即可.
A、B的直径上下一致,所以水的高度和时间之间对应的示意图为(2)、(3),由于A的直径小,B的直径大,A中水面上升的速度大于B,所以A对应(3),B对应(2),C为下大上小的锥形,随着水面的升高,横截面积越来越小,水面上升的速度会越来越快,故选(4),D的下部为圆球型,上部为圆柱形,随着水面的升高,横截面积越来越大,水面上升的速度会越来越慢,当达到球体的一半时,水面上升的速度会越来越快,所以水的高度和时间之间对应的示意图是(1).
故答案为:(A)——(3),(B)——(2),(C)——(4) , (D)——(1).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A的坐标为(3,﹣3),点B的坐标为(﹣1,3),回答下列问题
(1)点C的坐标是 .
(2)点B关于原点的对称点的坐标是 .
(3)△ABC的面积为 .
(4)画出△ABC关于x轴对称的△A′B′C′.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,△ABC中,AB=AC,∠B、∠C的平分线交于O点,过O点作EF∥BC交AB、AC于E、F.

(1)图①中有几个等腰三角形?猜想:EF与BE、CF之间有怎样的关系.
(2)如图②,若AB≠AC,其他条件不变,图中还有等腰三角形吗?如果有,分别指出它们.在第(1)问中EF与BE、CF间的关系还存在吗?
(3)如图③,若△ABC中∠B的平分线BO与三角形外角平分线CO交于O,过O点作OE∥BC交AB于E,交AC于F.这时图中还有等腰三角形吗?EF与BE、CF关系又如何?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在第一象限内,点P(2,3),M(a,2)是双曲线y= ![]() (k≠0)上的两点,PA⊥x轴于点A,MB⊥x轴于点B,PA与OM交于点C,则△OAC的面积为 .
(k≠0)上的两点,PA⊥x轴于点A,MB⊥x轴于点B,PA与OM交于点C,则△OAC的面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的运算程序中,若开始输入的![]() 值为
值为![]() ,我们发现第
,我们发现第![]() 次输出的结果为
次输出的结果为![]() ,第
,第![]() 次输出的结果为
次输出的结果为![]() ,……第
,……第![]() 次输出的结果_______________;第
次输出的结果_______________;第![]() 次输出的结果为______________.
次输出的结果为______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示.在△ABC中,∠BAC=106°,EF、MN分别是AB、AC的中垂线,E、N在BC上,则∠EAN=( )

A. 58° B. 32° C. 36° D. 34°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将一个长为4a,宽为2b的长方形,沿图中虚线均分成4个长方形,然后按图2形状拼成一个正方形.
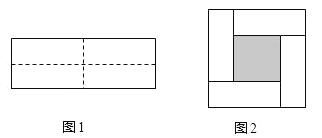
(1)图2中阴影部分的边长是 (用含a、b的式子表示);
(2)若2a+b=7,且ab=3,求图2中阴影部分的面积;
(3)观察图2,用等式表示出(2a﹣b)2,ab,(2a+b)2的数量关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】爱好思考的小茜在探究两条直线的位置关系查阅资料时,发现了“中垂三角形”,即两条中线互相垂直的三角形称为“中垂三角形”.如图(1)、图(2)、图(3)中,AM、BN是△ABC的中线,AM⊥BN于点P,像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.
(1)【特例探究】
如图1,当tan∠PAB=1,c=4 ![]() 时,a= , b=;
时,a= , b=;
如图2,当∠PAB=30°,c=2时,a= , b=;
(2)【归纳证明】
请你观察(1)中的计算结果,猜想a2、b2、c2三者之间的关系,用等式表示出来,并利用图3证明你的结论.
(3)【拓展证明】
如图4,ABCD中,E、F分别是AD、BC的三等分点,且AD=3AE,BC=3BF,连接AF、BE、CE,且BE⊥CE于E,AF与BE相交点G,AD=3 ![]() ,AB=3,求AF的长.
,AB=3,求AF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com