
【题目】如图1,将一个长为4a,宽为2b的长方形,沿图中虚线均分成4个长方形,然后按图2形状拼成一个正方形.
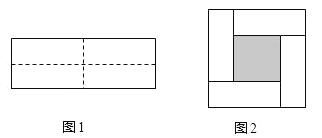
(1)图2中阴影部分的边长是 (用含a、b的式子表示);
(2)若2a+b=7,且ab=3,求图2中阴影部分的面积;
(3)观察图2,用等式表示出(2a﹣b)2,ab,(2a+b)2的数量关系是 .
【答案】(1)2a-b;(2)25;(3)(2a+b)2﹣(2a﹣b)2=8ab.
【解析】
(1)观察由已知图形,得到四个小长方形的长为2a,宽为b,那么图2中的空白部分的正方形的边长是小长方形的长减去小长方形的宽.
(2)通过观察图形,大正方形的边长为小长方形的长和宽的和.图2中空白部分的正方形的面积为大正方形的面积减去四个小长方形的面积.
(3)通过观察图形知:(2a+b)2,(2a-b)2, 8ab.分别表示的是大正方形、空白部分的正方形及小长方形的面积.
(1)图2的阴影部分的边长是2a﹣b.
故答案为:2a﹣b;
(2)由图2可知,阴影部分的面积=大正方形的面积﹣4个小长方形的面积.
∵大正方形的边长=2a+b=7,∴大正方形的面积=(2a+b)2=49.
又∵4个小长方形的面积之和=大长方形的面积=4a×2b=8ab=8×3=24,∴阴影部分的面积=(2a﹣b)2=49﹣24=25;
(3)由图2可以看出,大正方形面积=阴影部分的正方形的面积+四个小长方形的面积,即:(2a+b)2﹣(2a﹣b)2=8ab.
故答案为:(2a+b)2﹣(2a﹣b)2=8ab.


科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD中,点E在边BC上,点F在BA的延长线上,BE=AF,CF∥AE,CF与边AD相交于点G. 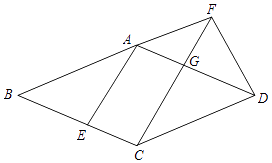
求证:
(1)FD=CG;
(2)CG2=FGFC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水滴进的玻璃容器如下图所示(水滴的速度是相同的),那么水的高度h是如何随着时间t变化的,请选择匹配的示意图与容器.
(A)——( ) (B)——( )
(C)——( ) (D)——( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方体的长为15宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )

A. 20 B. 25 C. 30 D. 32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“中华人民共和国道路交通管理条例”规定:小汽车在城市街道上行驶速度不得超过70 km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方30 m处,过了2 s后,测得小汽车与车速检测仪间距离为50 m,这辆小汽车超速了吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校篮球社团决定购买运动装备。经了解,甲、乙两家运动产品经销店以同样的价格出售某种品牌的队服和篮球,已知每套队服比每个篮球多![]() 元,两套队服与三个篮球的费用相等.经洽谈,甲店的优惠方案是:每购买十套队服,送一个篮球,乙店的优惠方案是:若购买队服超过
元,两套队服与三个篮球的费用相等.经洽谈,甲店的优惠方案是:每购买十套队服,送一个篮球,乙店的优惠方案是:若购买队服超过![]() 套,则购买篮球打八折.
套,则购买篮球打八折.
(1)求每套队服和每个篮球的价格是多少?
(2)若篮球社团购买![]() 套队服和
套队服和![]() 个篮球(
个篮球(![]() 是大于
是大于![]() 的整数),请用含
的整数),请用含![]() 的式子分别表示出到甲经销店和乙经销店购买装备所花的费用;
的式子分别表示出到甲经销店和乙经销店购买装备所花的费用;
(3)在(2)的条件下,若![]() ,通过计算判断到甲、乙哪家经销店购买更划算。
,通过计算判断到甲、乙哪家经销店购买更划算。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某校准备组织学生及学生家长坐高铁到杭州进行社会实践,为了便于管理.所有人员必须乘坐在同一列高铁上.根据报名人数,若都买一等座单程火车票需6560元,若都买二等座单程火车票,则需3120元(学生票二等座打7.5折,一等座不打折).已知学生家长与教师的人数之比为3:1,余姚北站到杭州东站的火车票价格如表所示:
运行区间 | 票价 | ||
上车站 | 下车站 | 一等座 | 二等座 |
余姚北 | 杭州东 | 82(元) | 48(元) |
(1)参加社会实践的老师、家长与学生各有多少人?
(2)由于各种原因,二等座火车票单程只能买m张(m小于参加社会实践的人数),其余的须买一等座火车票,在保证每位参与人员都有座位坐的前提下,请你设计最经济的购票方案,并写出购买火车票的总费用(单程)y(元)(用含m的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知线段AB=16cm,点C为线段AB上的一个动点,点D、E分别是AC和BC的中点.

(1)若点C恰为AB的中点,求DE的长;
(2)若AC=6cm,求DE的长;
(3)试说明不论AC取何值(不超过16cm),DE的长不变;
(4)知识迁移:如图2,已知∠AOB=130°,过角的内部任一点C画射线OC,若OD、OE分别平分∠AOC和∠BOC,试说明∠DOE=65°与射线OC的位置无关.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com