
【题目】如图,直线AB、CD相交于点O,过点O作两条射线OM、ON,且∠AOM=∠CON=90°

(1)若OC平分∠AOM,求∠AOD的度数.
(2)若∠1=![]() ∠BOC,求∠AOC和∠MOD.
∠BOC,求∠AOC和∠MOD.
【答案】(1) 135°;(2) ∠AOC=60° ;∠MOD=150°.
【解析】
(1)根据OC平分∠AOM,易得∠1=∠AOC=45°,再由平角可求出∠AOD的度数
(2)由题目中给出的∠1=![]() ∠BOC和∠AOM=90°,可求出∠1的度数,进而再求出∠AOC和∠MOD的度数.
∠BOC和∠AOM=90°,可求出∠1的度数,进而再求出∠AOC和∠MOD的度数.
(1)∠AOM=∠CON=90°,OC平分∠AOM
∴∠1=∠AOC=45°
∴∠AOD=180°-∠AOC=180°-45°=135°;
(2)∵∠AOM=90°
∴∠BOM=180°-90°=90°
∵∠1=![]() ∠BOC
∠BOC
∴∠1=![]() ∠BOM=30°
∠BOM=30°
∴∠AOC=90°-30°=60°,∠MOD=180°-30°=150°.
故答案是:(1)∠AOD=135°;(2) ∠AOC=60° ;∠MOD=150°.


科目:初中数学 来源: 题型:
【题目】观察下列等式:
第一个等式: ![]()
第二个等式: ![]()
第三个等式: ![]()
第四个等式: ![]()
则式子![]() __________________;
__________________;
用含n的代数式表示第n个等式: ![]() ____________________________;
____________________________;
查看答案和解析>>
科目:初中数学 来源: 题型:
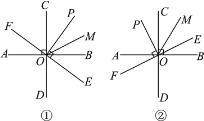
【题目】如图,已知O为直线AB上的一点,CD⊥AB于点O,PO⊥OE于点O,OM平分∠COE,点F在OE的反向延长线上.
(1)当OP在∠BOC内,OE在∠BOD内时,如图①所示,直接写出∠POM和∠COF之间的数量关系;
(2)当OP在∠AOC内且OE在∠BOC内时,如图②所示,试问(1)中∠POM和∠COF之间的数量关系是否发生变化?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形OABC的OA边在x轴的正半轴上,OC在y轴的正半轴上,抛物线y=ax2+bx经过点B(1,4)和点E(3,0)两点.
(1)求抛物线的解析式;
(2)若点D在线段OC上,且BD⊥DE,BD=DE,求D点的坐标;
(3)在条件(2)下,在抛物线的对称轴上找一点M,使得△BDM的周长为最小,并求△BDM周长的最小值及此时点M的坐标;
(4)在条件(2)下,从B点到E点这段抛物线的图象上,是否存在一个点P,使得△PAD的面积最大?若存在,请求出△PAD面积的最大值及此时P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年宁波市北仑区体育中考的3个选测项目分别是50米跑,一分钟跳绳,篮球运球投篮.另规定:游泳满分的学生,只需从3个选测项目中选择一项进行测试;游泳未得满分或未参加的学生,需从3个选测项目中任选两项进行测试.
(1)小明因游泳测试获得了满分,求他在3个选测项目中选择“一分钟跳绳”项目的概率.
(2)若小红和小慧的游泳测试都未得满分,她们都必须从3个选测项目中选择两项进行体育中考测试,请用列表(或画树状图)的方法,求出小红和小慧选择的两个项目完全相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在Rt△ABC和Rt△BCD中,∠ABC=∠BCD=90°,BD与AC相交于点E,AB=9,cos∠BAC= ![]() ,tan∠DBC=
,tan∠DBC= ![]() .
. 
求:
(1)边CD的长;
(2)△BCE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,△ABC中,AB=AC,∠B、∠C的平分线交于O点,过O点作EF∥BC交AB、AC于E、F.

(1)图①中有几个等腰三角形?猜想:EF与BE、CF之间有怎样的关系.
(2)如图②,若AB≠AC,其他条件不变,图中还有等腰三角形吗?如果有,分别指出它们.在第(1)问中EF与BE、CF间的关系还存在吗?
(3)如图③,若△ABC中∠B的平分线BO与三角形外角平分线CO交于O,过O点作OE∥BC交AB于E,交AC于F.这时图中还有等腰三角形吗?EF与BE、CF关系又如何?说明你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com