
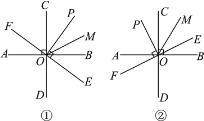
【题目】如图,已知O为直线AB上的一点,CD⊥AB于点O,PO⊥OE于点O,OM平分∠COE,点F在OE的反向延长线上.
(1)当OP在∠BOC内,OE在∠BOD内时,如图①所示,直接写出∠POM和∠COF之间的数量关系;
(2)当OP在∠AOC内且OE在∠BOC内时,如图②所示,试问(1)中∠POM和∠COF之间的数量关系是否发生变化?并说明理由.
【答案】(1)∠POM=![]() ∠COF,理由见解析;(2)∠POM=
∠COF,理由见解析;(2)∠POM=![]() ∠COF,理由见解析
∠COF,理由见解析
【解析】
(1)利用垂直的定义,CD⊥AB,PO⊥EO,等量代换得∠COP=∠BOE,利用角平分线的性质,得∠POM=![]() ∠POB=
∠POB=![]() (90°-∠POC),∠COF=90°-∠COP,得出结论;
(90°-∠POC),∠COF=90°-∠COP,得出结论;
(2)利用垂直的定义,同角的余角相等可得∠COP=∠AOF,可推出∠COP+∠COB=∠AOF+∠AOC,即∠BOP=∠COF,由对顶角相等得∠AOF=∠BOE=∠COP,利用角平分线的性质,得∠COP+∠COM=∠BOE+∠MOE,即∠POM=![]() ∠BOP,等量代换得出结论.
∠BOP,等量代换得出结论.
解:(1)∠POM=![]() ∠COF.
∠COF.
证明:∵CD⊥AB,
∴∠COP+∠BOP=90°,
∵OP⊥OE,
∴∠BOE+∠BOP=90°,
∴∠COP=∠BOE,
∵OM平分∠COE,
∴∠POM=∠MOB=![]() ∠POB=
∠POB=![]() (90°∠POC),
(90°∠POC),
∵∠COF=90°∠COP,
∴∠POM=![]() ∠COF;
∠COF;
(2)不发生变化.理由:∵CD⊥AB于点O,
∴∠AOP+∠COP=90°.
∵PO⊥OE于点O,
∴∠AOP+∠AOF=90°,
∴∠COP=∠AOF.
又∵∠AOC=∠COB=90°,
∴∠COP+∠COB=∠AOF+∠AOC,
即∠BOP=∠COF.
∵∠AOF=∠BOE,∴∠COP=∠BOE.
∵OM平分∠COE,∴∠COM=∠MOE,
∴∠COP+∠COM=∠BOE+∠MOE,
∴∠POM=![]() ∠BOP,
∠BOP,
∴∠POM=![]() ∠COF.
∠COF.
故答案为:(1)∠POM=![]() ∠COF,理由见解析;(2)∠POM=
∠COF,理由见解析;(2)∠POM=![]() ∠COF,理由见解析.
∠COF,理由见解析.


科目:初中数学 来源: 题型:
【题目】如图,在边长为8的正方形ABCD中,点O为AD上一动点(4<OA<8),以O为圆心,OA的长为半径的圆交边CD于点M,连接OM,过点M作⊙O的切线交边BC于N.
(1)求证:△ODM∽△MCN;
(2)设DM=x,OA=R,求R关于x的函数关系式;
(3)在动点O逐渐向点D运动(OA逐渐增大)的过程中,△CMN的周长如何变化?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点A为坐标原点,点B在x轴正半轴,点D在y轴正半轴,点C坐标为(6,m),点E是CD的中点,以CE为一边在矩形ABCD的内部作矩形CEFG,使点F在直线y=x上,交线段BC于点G,直线DG的函数表达式为y=- ![]() x+4,直线DG和AF交于点H.
x+4,直线DG和AF交于点H.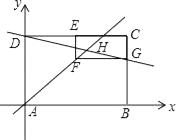
(1)求m的值;
(2)求点H的坐标;
(3)判断直线BE是否经过点H,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O的内接四边形ACDB中,AB为直径,AC:BC=1:2,点D为弧AB的中点,BE⊥CD垂足为E. 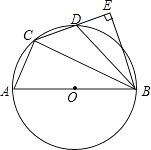
(1)求∠BCE的度数;
(2)求证:D为CE的中点;
(3)连接OE交BC于点F,若AB= ![]() ,求OE的长度.
,求OE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高中学校为使高一新生入校后及时穿上合身的校服,现提前对某校九年级(3)班学生即将所穿校服型号情况进行了摸底调查,并根据调查结果绘制了如图两个不完整的统计图(校服型号以身高作为标准,共分为6种型号).
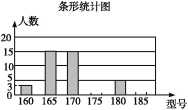
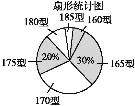
根据以上信息,解答下列问题:
(1)该班共有多少名学生?其中穿175型校服的学生有多少人?
(2)在条形统计图中,请把空缺的部分补充完整;
(3)在扇形统计图中,请计算185型校服所对应扇形圆心角的大小;
(4)求该班学生所穿校服型号的众数和中位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司招聘职员两名,对甲、乙、丙、丁四名候选人进行了笔试和面试,各项成绩满分均为100分,然后再按笔试占60%、面试占40%计算候选人的综合成绩(满分为100分).
他们的各项成绩如下表所示:
候选人 | 笔试成绩/分 | 面试成绩/分 |
甲 | 90 | 88 |
乙 | 84 | 92 |
丙 | x | 90 |
丁 | 88 | 86 |
(1)直接写出这四名候选人面试成绩的中位数;
(2)现得知候选人丙的综合成绩为87.6分,求表中x的值;
(3)求出其余三名候选人的综合成绩,并以综合成绩排序确定所要招聘的前两名的人选.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是橘子的销售额随橘子卖出质量的变化表:
质量/千克 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | … |
销售额/元 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | … |
(1)这个表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当橘子卖出5千克时,销售额是_______元.
(3)如果用![]() 表示橘子卖出的质量,
表示橘子卖出的质量,![]() 表示销售额,按表中给出的关系,
表示销售额,按表中给出的关系,![]() 与
与![]() 之间的关系式为______.
之间的关系式为______.
(4)当橘子的销售额是100元时,共卖出多少千克橘子?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,过点O作两条射线OM、ON,且∠AOM=∠CON=90°

(1)若OC平分∠AOM,求∠AOD的度数.
(2)若∠1=![]() ∠BOC,求∠AOC和∠MOD.
∠BOC,求∠AOC和∠MOD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD中,点E在边BC上,点F在BA的延长线上,BE=AF,CF∥AE,CF与边AD相交于点G. 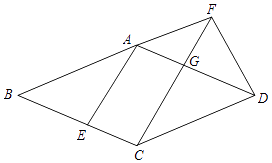
求证:
(1)FD=CG;
(2)CG2=FGFC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com