
【题目】如图,在⊙O的内接四边形ACDB中,AB为直径,AC:BC=1:2,点D为弧AB的中点,BE⊥CD垂足为E. 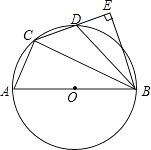
(1)求∠BCE的度数;
(2)求证:D为CE的中点;
(3)连接OE交BC于点F,若AB= ![]() ,求OE的长度.
,求OE的长度.
【答案】
(1)解:连接AD,
∵D为弧AB的中点,
∴AD=BD,
∵AB为直径,
∴∠ADB=90°,
∴∠DAB=∠DBA=45°,
∴∠DCB=∠DAB=45°
(2)证明:∵BE⊥CD,又∵∠ECB=45°,
∴∠CBE=45°,
∴CE=BE,
∵四边形ACDB是圆O的内接四边形,
∴∠A+∠BDC=180°,
又∵∠BDE+∠BDC=180°,
∴∠A=∠BD,
又∵∠ACB=∠BED=90°,
∴△ABC∽△DBE,
∴DE:AC=BE:BC,
∴DE:BE=AC:BC=1:2,
又∵CE=BE,
∴DE:CE=1:2,
∴D为CE的中点
(3)解:连接EO,
∵CO=BO,CE=BE,
∴OE垂直平分BC,
∴F为BC中点,
又∵O为AB中点,
∴OF为△ABC的中位线,
∴OF= ![]() AC,
AC,
∵∠BEC=90°,EF为中线,
∴EF= ![]() BC,
BC,
在Rt△ACB中,AC2+BC2=AB2,
∵AC:BC=1:2,AB= ![]() ,
,
∴AC= ![]() ,BC=2
,BC=2 ![]() ,
,
∴OE=OF+EF= ![]() .
.
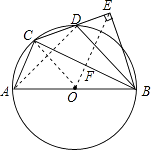
【解析】(1)连接AD,由D为弧AB的中点,得到AD=BD,根据圆周角定理即可得到结论;(2)由已知条件得到∠CBE=45°,根据圆内接四边形的性质得到∠A=∠BD,根据相似三角形的性质得到DE:AC=BE:BC,即可得到结论.(3)连接CO,根据线段垂直平分线的判定定理得到OE垂直平分BC,由三角形的中位线到现在得到OF= ![]() AC,根据直角三角形的性质得到EF=
AC,根据直角三角形的性质得到EF= ![]() BC,由勾股定理即可得到结论.
BC,由勾股定理即可得到结论.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:
【题目】观察下列等式:
第一个等式: ![]()
第二个等式: ![]()
第三个等式: ![]()
第四个等式: ![]()
则式子![]() __________________;
__________________;
用含n的代数式表示第n个等式: ![]() ____________________________;
____________________________;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两台机床同时生产同一种零件,在10天中两台机床每天生产的次品数如下:
甲:0,1,0,2,2,0,3,1,2,4;
乙:2,3,1,1,0,2,1,1,0,1.
(1)分别计算两组数据的平均数和方差;
(2)从结果看,在10天中哪台机床出现次品的波动较小?
(3)由此推测哪台机床的性能较好
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(7分)某学校举行演讲比赛,选出了10名同学担任评委,并事先拟定从如下4个方案中选择合理的方案来确定每个演讲者的最后得分(满分为10分):
方案1:所有评委所给分的平均数,
方案2:在所有评委所给分中,去掉一个最高分和一个最低分.然后再计算其余给分的l平均数.
方案3:所有评委所给分的中位效.
方案4:所有评委所给分的众数.
为了探究上述方案的合理性.先对某个同学的演讲成绩进行了统计实验.下面是这个同学的得分统计图:

(1)分别按上述4个方案计算这个同学演讲的最后得分;
(2)根据(1)中的结果,请用统计的知识说明哪些方案不适台作为这个同学演讲的最后得分,并给出该同学的最后得分.
查看答案和解析>>
科目:初中数学 来源: 题型:
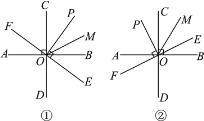
【题目】如图,已知O为直线AB上的一点,CD⊥AB于点O,PO⊥OE于点O,OM平分∠COE,点F在OE的反向延长线上.
(1)当OP在∠BOC内,OE在∠BOD内时,如图①所示,直接写出∠POM和∠COF之间的数量关系;
(2)当OP在∠AOC内且OE在∠BOC内时,如图②所示,试问(1)中∠POM和∠COF之间的数量关系是否发生变化?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形OABC的OA边在x轴的正半轴上,OC在y轴的正半轴上,抛物线y=ax2+bx经过点B(1,4)和点E(3,0)两点.
(1)求抛物线的解析式;
(2)若点D在线段OC上,且BD⊥DE,BD=DE,求D点的坐标;
(3)在条件(2)下,在抛物线的对称轴上找一点M,使得△BDM的周长为最小,并求△BDM周长的最小值及此时点M的坐标;
(4)在条件(2)下,从B点到E点这段抛物线的图象上,是否存在一个点P,使得△PAD的面积最大?若存在,请求出△PAD面积的最大值及此时P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在Rt△ABC和Rt△BCD中,∠ABC=∠BCD=90°,BD与AC相交于点E,AB=9,cos∠BAC= ![]() ,tan∠DBC=
,tan∠DBC= ![]() .
. 
求:
(1)边CD的长;
(2)△BCE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com