
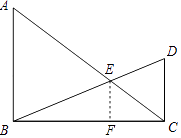
【题目】已知:如图,在Rt△ABC和Rt△BCD中,∠ABC=∠BCD=90°,BD与AC相交于点E,AB=9,cos∠BAC= ![]() ,tan∠DBC=
,tan∠DBC= ![]() .
. 
求:
(1)边CD的长;
(2)△BCE的面积.
【答案】
(1)解:∵∠ABC=∠BCD=90°,AB=9,cos∠BAC= ![]() ,tan∠DBC=
,tan∠DBC= ![]() ,
,
∴设CD=5a,则BC=12a,AB=9a,
∴9a=9,得a=1,
∴CD=5a=5,
即CD的长是5
(2)解:由(1)知,AB=9,BC=12,CD=5,
∵∠ABC=∠BCD=90°,
∴AB∥CD,
∴ ![]() ,
,
作EF∥AB交CB于点F,
则△CEF∽△CAB,
∴ ![]() ,
,
∴ ![]() ,
,
解得,EF= ![]() ,
,
∴△BCE的面积是: 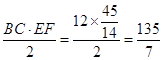 .
.
【解析】(1)根据题目中的数据和锐角三角函数可以求得CD的长;(2)根据题意可以求得BC和BC边上的高,从而可以求得△BCE的面积.
【考点精析】本题主要考查了解直角三角形的相关知识点,需要掌握解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,在⊙O的内接四边形ACDB中,AB为直径,AC:BC=1:2,点D为弧AB的中点,BE⊥CD垂足为E. 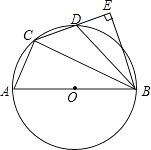
(1)求∠BCE的度数;
(2)求证:D为CE的中点;
(3)连接OE交BC于点F,若AB= ![]() ,求OE的长度.
,求OE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,过点O作两条射线OM、ON,且∠AOM=∠CON=90°

(1)若OC平分∠AOM,求∠AOD的度数.
(2)若∠1=![]() ∠BOC,求∠AOC和∠MOD.
∠BOC,求∠AOC和∠MOD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】基本图形:在Rt△![]() 中,
中,![]() ,
,![]() 为
为![]() 边上一点(不与点
边上一点(不与点![]() ,
,![]() 重合),将线段
重合),将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() .
.
探索:(1)连接![]() ,如图①,试探索线段
,如图①,试探索线段![]() 之间满足的等量关系,并证明结论;
之间满足的等量关系,并证明结论;
(2)连接![]() ,如图②,试探索线段
,如图②,试探索线段![]() 之间满足的等量关系,并证明结论;
之间满足的等量关系,并证明结论;

联想:(3)如图③,在四边形![]() 中,
中,![]() .若
.若![]() ,
,![]() ,则
,则![]() 的长为 .
的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为庆祝“六一”儿童节,某市中小学统一组织文艺汇演,甲、乙两所学校共92人(其中甲校的人数多于乙校的人数,且甲校的人数不足90人)准备统一购买服装参加演出;下面是某服装厂给出的演出服装的价格表
购买服装的套数 | 1套至45套 | 46套至90套 | 91套以上 |
每套服装的价格 | 60元 | 50元 | 40元 |
(1)如果两所学校分别单独购买服装一共应付5000元,甲、乙两所学校各有多少学生准备参加演出?
(2)如果甲校有10名同学抽调去参加书法绘画比赛不能参加演出,请你为两所学校设计一种最省钱的购买服装方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD中,点E在边BC上,点F在BA的延长线上,BE=AF,CF∥AE,CF与边AD相交于点G. 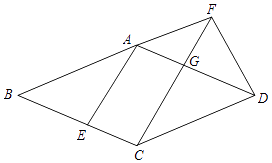
求证:
(1)FD=CG;
(2)CG2=FGFC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方体的长为15宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )

A. 20 B. 25 C. 30 D. 32
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com