
����Ŀ����ͼ��������OABC��OA����x����������ϣ�OC��y����������ϣ�������y=ax2+bx������B��1��4���͵�E��3��0�����㣮
��1���������ߵĽ���ʽ��
��2������D���߶�OC�ϣ���BD��DE��BD=DE����D������ꣻ
��3����������2���£��������ߵĶԳ�������һ��M��ʹ�á�BDM���ܳ�Ϊ��С�������BDM�ܳ�����Сֵ����ʱ��M�����ꣻ
��4����������2���£���B�㵽E����������ߵ�ͼ���ϣ��Ƿ����һ����P��ʹ�á�PAD�������������ڣ��������PAD��������ֵ����ʱP������ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1���⣺����B��1��4����E��3��0����������������ߵĽ���ʽ�ã� ![]() ��
��
��ã� ![]() ��
��
�����ߵĽ���ʽΪy=��2x2+6x
��2���⣺��ͼ1��ʾ��

��BD��DE��
���BDE=90�㣮
���BDC+��EDO=90�㣮
�֡ߡ�ODE+��DEO=90�㣬
���BDC=��DE0��
�ڡ�BDC�͡�DOE�У� 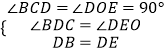 ��
��
���BDC�ա�DEO��
��OD=AO=1��
��D��0��1��
��3���⣺��ͼ2��ʾ������B���������ߵĶԳ���ĶԳƵ�B�䣬����B��D�������ߵĶԳ������M��
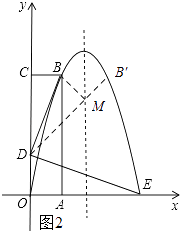
��x=�� ![]() =
= ![]() ��
��
���B���������2��4����
�ߵ�B���B�����x= ![]() �Գƣ�
�Գƣ�
��MB=B��M��
��DM+MB=DM+MB�䣮
�൱��D��M��B����һ��ֱ����ʱ��MD+MB����Сֵ������BMD���ܳ�����Сֵ����
���������ľ��빫ʽ��֪��BD= ![]() =
= ![]() ��DB��=
��DB��= ![]() =
= ![]() ��
��
���BDM����Сֵ= ![]() +
+ ![]() ��
��
��ֱ��B��D�Ľ���ʽΪy=kx+b��
����D��B����������ã� ![]() ��
��
��ã�k= ![]() ��b=1��
��b=1��
��ֱ��DB��Ľ���ʽΪy= ![]() x+1��
x+1��
��x= ![]() ����ã�y=
����ã�y= ![]() ��
��
��M�� ![]() ��
�� ![]() ��
��
��4���⣺��ͼ3��ʾ������F��FG��x�ᣬ����ΪG��
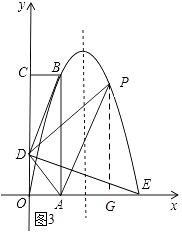
���P��a����2a2+6a������OG=a��PG=��2a2+6a��
��S����DOGP= ![]() ��OD+PG��OG=
��OD+PG��OG= ![]() ����2a2+6a+1����a=��a3+3a2+
����2a2+6a+1����a=��a3+3a2+ ![]() a��S��ODA=
a��S��ODA= ![]() ODOA=
ODOA= ![]() ��1��1=
��1��1= ![]() ��S��AGP=
��S��AGP= ![]() AGPG=��a3+4a2��3a��
AGPG=��a3+4a2��3a��
��S��PDA=S����DOGP��S��ODA��S��AGP=��a2+ ![]() a��
a�� ![]() ��
��
�൱a= ![]() ʱ��S��PDA�����ֵΪ
ʱ��S��PDA�����ֵΪ ![]() ��
��
���P�������� ![]() ��
�� ![]() ��
��
����������1������B��1��4����E��3��0����������������ߵĽ���ʽ���õ�����a��b�ķ����飬���a��b��ֵ���Ӷ��ɵõ������ߵĽ���ʽ����2������ͬ�ǵ�������֤����BDC=��DE0��Ȼ��������AAS֤����BDC�ա�DEO���Ӷ��õ�OD=AO=1�����ǿ���õ�D�����ꣻ��3������B���������ߵĶԳ���ĶԳƵ�B�䣬����B��D�������ߵĶԳ������M������������ߵĶԳ��᷽�̣��Ӷ��õ���B������꣬����ԳƵ����ʿ�֪����D��M��B����һ��ֱ����ʱ����BMD���ܳ�����Сֵ�����������ľ��빫ʽ���BD��B��D�ij��ȣ��Ӷ��õ������ε��ܳ���Сֵ��Ȼ�����ݴ���ϵ�������D��B��Ľ���ʽ��Ȼ��M�ĺ�����������õ�M�������ꣻ��4������F��FG��x�ᣬ����ΪG�����F��a����2a2+6a������OG=a��FG=��2a2+6a��Ȼ������S��FDA=S����DOGF��S��ODA��S��AGF�������ε������a�ĺ�����ϵʽ��Ȼ�����ݶ��κ�����������⼴�ɣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ǰѶŸ�(����)�������з���ƽ��ֱ������ϵ�У�

(1)���������������������������������ǣ�______��______��________����
(2)����1�����3�жԵ����ٽ���4�����6�жԵ����������ɿ�ʼ������________���α任����________��________��
(3)��������ʼ��������(1��1)��ʹ�������굽(3��2)��Ӧ�������жԵ���ͬʱ�����жԵ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�O���ڽ��ı���ACDB�У�ABΪֱ����AC��BC=1��2����DΪ��AB���е㣬BE��CD����ΪE�� 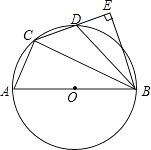
��1�����BCE�Ķ�����
��2����֤��DΪCE���е㣻
��3������OE��BC�ڵ�F����AB= ![]() ����OE�ij��ȣ�
����OE�ij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾��ƸְԱ����,�Լס��ҡ�������������ѡ�˽����˱��Ժ�����,����ɼ����־�Ϊ100��,Ȼ���ٰ�����ռ60%������ռ40%�����ѡ�˵��ۺϳɼ�(����Ϊ100��).
���ǵĸ���ɼ����±���ʾ:
��ѡ�� | ���Գɼ�/�� | ���Գɼ�/�� |
�� | 90 | 88 |
�� | 84 | 92 |
�� | x | 90 |
�� | 88 | 86 |
(1)ֱ��д����������ѡ�����Գɼ�����λ��;
(2)�ֵ�֪��ѡ�˱����ۺϳɼ�Ϊ87.6��,�����x��ֵ;
(3)�������������ѡ�˵��ۺϳɼ�,�����ۺϳɼ�����ȷ����Ҫ��Ƹ��ǰ��������ѡ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���±������ӵ����۶����������������ı仯����
����/ǧ�� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | �� |
���۶�/Ԫ | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | �� |
��1���������ӳ������������֮��Ĺ�ϵ���ĸ����Ա������ĸ����������
��2������������5ǧ��ʱ�����۶���_______Ԫ.
��3�������![]() ��ʾ����������������
��ʾ����������������![]() ��ʾ���۶�����и����Ĺ�ϵ��
��ʾ���۶�����и����Ĺ�ϵ��![]() ��
��![]() ֮��Ĺ�ϵʽΪ______.
֮��Ĺ�ϵʽΪ______.
��4�������ӵ����۶���100Ԫʱ������������ǧ�����ӣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���˷���ʽ��̽����Ӧ��.
(1)��ͼ1�����������Ӱ���ֵ������ (д������ƽ�������ʽ)��
(2)��ͼ2��������Ӱ���ֲü�����������ƴ��һ�����Σ����Ŀ��� ������ ������� (д�ɶ���ʽ�˷�����ʽ)��
(3)�Ƚ�ͼ1��ͼ2��ͼ����Ӱ������������Եõ��˷���ʽ (��ʽ�ӱ���)��
(4)���������õ��Ĺ�ʽ���������и��⣺
��(2m+n-p)(2m-n+p)����10.3��9.7.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��AB��CD�ཻ�ڵ�O������O����������OM��ON������AOM����CON��90��

(1)��OCƽ����AOM������AOD�Ķ�����
(2)����1��![]() ��BOC������AOC����MOD.
��BOC������AOC����MOD.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ�Σ���Rt��![]() �У�
��![]() ��
��![]() Ϊ
Ϊ![]() ����һ�㣨�����
����һ�㣨�����![]() ��
��![]() �غϣ������߶�
�غϣ������߶�![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() �õ�
�õ�![]() .
.
̽������1������![]() ����ͼ�٣���̽���߶�
����ͼ�٣���̽���߶�![]() ֮������ĵ�����ϵ����֤�����ۣ�
֮������ĵ�����ϵ����֤�����ۣ�
��2������![]() ����ͼ�ڣ���̽���߶�
����ͼ�ڣ���̽���߶�![]() ֮������ĵ�����ϵ����֤�����ۣ�
֮������ĵ�����ϵ����֤�����ۣ�

��������3����ͼ�ۣ����ı���![]() �У�
��![]() ����
����![]() ��
��![]() ����
����![]() �ij�Ϊ .
�ij�Ϊ .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�κ���ͼ��x���ڵ�(��2,0)����y��Ľ��㵽ԭ��ľ���Ϊ5�����һ�κ�������ʽΪ________��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com