Question

【题目】如图，平面直角坐标系中，O为菱形ABCD的对称中心，已知C（2，0），D（0，﹣1），N为线段CD上一点（不与C、D重合）．

（1）求以C为顶点，且经过点D的抛物线解析式；
（2）设N关于BD的对称点为N1 ， N关于BC的对称点为N2 ， 求证：△N1BN2∽△ABC；
（3）求（2）中N1N2的最小值；
（4）过点N作y轴的平行线交（1）中的抛物线于点P，点Q为直线AB上的一个动点，且∠PQA=∠BAC，求当PQ最小时点Q坐标．

Answer 1

【答案】
（1）解：由已知，设抛物线解析式为y=a（x﹣2）2

把D（0，﹣1）代入，得a=﹣

∴y=﹣ （x﹣2）2

（2）解：如图1，连结BN．

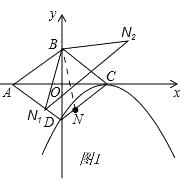
∵N1，N2是N的对称点

∴BN1=BN2=BN，∠N1BD=∠NBD，∠NBC=∠N2BC

∴∠N1BN2=2∠DBC

∵四边形ABCD是菱形

∴AB=BC，∠ABC=2∠DBC

∴∠ABC=∠N1BN2，

∴△ABC∽△N1BN2

（3）解：∵点N是CD上的动点，

∴点到直线的距离，垂线段最短，

∴当BN⊥CD时，BN最短．

∵C（2，0），D（0，﹣1）

∴CD= ，

∴BNmin= ，

∴BN1min=BNmin= ，

∵△ABC∽△N1BN2

∴ ，

N1N2min=

（4）解：如图2，

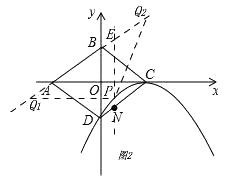
过点P作PE⊥x轴，交AB于点E．

∵∠PQA=∠BAC

∴PQ1∥AC

∵菱形ABCD中，C（2，0），D（0，﹣1）

∴A（﹣2，0），B（0，1）

∴lAB：Y= x+1

不妨设P（m，﹣ （m﹣2）2），则E（m， m+1）

∴PE= m2﹣ m+2

∴当m=1时，

此时，PQ1最小，最小值为 = ，

∴PQ1=PQ2=

【解析】（1）由抛物线顶点在x轴上，可得抛物线可设为y=a(x-h)2再由顶点坐标C（2，0），点D（0，﹣1）利用待定系数法易得解析式为y=﹣ （x﹣2）2。
（2）由对称易得BN1=BN2=BN，又AB=BC可得对应边成比例，又由对称易得∠ABC=∠N1BN2可证△ABC∽△N1BN2。
（3）由（2）△ABC∽△N1BN2，由于三边比不变，所以BN1最小时，可得N1N2最小；由点与直线之间，垂线段最短，易得BN1⊥AD时最短，所以最后得证N1N2最小值。
（4）由所给条件∠PQA=∠BAC可得PQ1∥AC又已知菱形ABCD中，C（2，0），D（0，﹣1）可得A（﹣2，0），B（0，1）得到直线AB的解析式lAB：Y= x+1；若设P（m，﹣ （m﹣2）2），则可由点Q为直线AB上的一个动点得E（m， m+1），则PE为纵坐标的差PE= m2﹣ m+2；此时PQ1最小，易由三角函数可得PQ1=PQ2=

【考点精析】本题主要考查了二次函数的图象和二次函数的性质的相关知识点，需要掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小才能正确解答此题．