
【题目】已知:如图,点C在AOB的一边OA上,过点C的直线DE//OB,CF平分ACD,CG CF于C .
(1)若O =40,求ECF的度数;
(2)求证:CG平分OCD;
(3)当O为多少度时,CD平分OCF,并说明理由.

【答案】(1)ECF=![]() ;
;
(2)证明见解析;
(3)结论:当O=60时 ,CD平分OCF,理由见解析.
【解析】试题分析:由两直线平行,同位角相等得∠ACE =40,由平角定义得∠ACD=![]() ,再由角平分线定义得
,再由角平分线定义得![]() ,由邻补角定义得到ECF=
,由邻补角定义得到ECF=![]() ;(2)由垂直的定义得
;(2)由垂直的定义得![]() ,由
,由![]() 得
得![]() ,由等角的余角相等可证;(3)由两直线平行,同位角相等得∠DCO=∠O=60,由角平分线性质得∠DCF=60,由等量代换得
,由等角的余角相等可证;(3)由两直线平行,同位角相等得∠DCO=∠O=60,由角平分线性质得∠DCF=60,由等量代换得![]() 即可得证.
即可得证.
试题解析:(1)∵DE//OB ,
∴∠O=∠ACE,(两直线平行,同位角相等)
∵O =40,
∴∠ACE =40,
∵∠ACD+∠ACE=![]() (平角定义)
(平角定义)
∴ ∠ACD=![]()
又 ∵CF平分ACD ,
∴![]() (角平分线定义)
(角平分线定义)
∴ ECF=![]()
(2)证明:∵CG CF,
∴![]() .
.
∴![]()
又 ∵![]()
![]() )
)
∴![]()
∵![]()
∴![]() (等角的余角相等)
(等角的余角相等)
即CG平分OCD .
(3)结论:当O=60时 ,CD平分OCF .
当O=60时
∵DE//OB,
∴ ∠DCO=∠O=60.
∴ ∠ACD=120.
又 ∵CF平分ACD
∴ ∠DCF=60,
∴![]()
即CD平分OCF .


科目:初中数学 来源: 题型:
【题目】甲、乙两人进行射击测试,每人20次射击的平均成绩恰好相等,且他们的标准差分别是S甲=1.8,S乙=0.7.在本次射击测试中,甲、乙两人中成绩较为稳定的是_____.(填:甲或乙)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的对话。
小红:“售货员,我要买些梨。”
售货员说:“小红,你上次买的那种梨卖完了,我们还没来得及进货,我建议你这次买些新进的苹果,价格比梨贵一点,不过这批苹果的味道挺好哟!”
小红:“好,这次和上次一样,也花30元。”
对照前后两次的电脑小票,小红发现,每千克苹果的单价是梨的1.5倍,买的苹果的重量比梨轻2.5Kg。
试根据上面的对话和小红的发现,分别求出苹果和梨的单价。
查看答案和解析>>
科目:初中数学 来源: 题型:
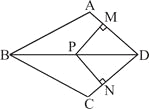
【题目】在四边形ABCD中,AB=BC,对角线BD平分![]() ,P是BD上一点,过P作PM⊥AD于点M,PN⊥CD于点N.
,P是BD上一点,过P作PM⊥AD于点M,PN⊥CD于点N.
(1)求证: ![]() ;
;
(2)若![]() ,求证:四边形MPND是正方形。
,求证:四边形MPND是正方形。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com