
【题目】如果关于![]() 的一元二次方程
的一元二次方程![]() 有两个实数根,且其中一根为另一根的2倍,则称这样的方程为“倍根方程”,以下关于倍根方程的说法,不正确的是( )
有两个实数根,且其中一根为另一根的2倍,则称这样的方程为“倍根方程”,以下关于倍根方程的说法,不正确的是( )
A.方程![]() 是倍根方程;
是倍根方程;
B.若![]() 是倍根方程,则
是倍根方程,则![]() ;
;
C.若方程![]() 是倍根方程,且相异两点
是倍根方程,且相异两点![]() 都在抛物线
都在抛物线![]() 上,则方程
上,则方程![]() 的一个根为
的一个根为![]() ;
;
D.若点![]() 在反比例函数
在反比例函数![]() 的图象上,则关于
的图象上,则关于![]() 的方程
的方程![]() 是倍根方程.
是倍根方程.
【答案】C
【解析】
A、根据倍根方程定义即可得到方程x2+3x+2=0是倍根方程;
B、根据(x-2)(mx+n)=0是倍根方程,且x1=2,x2=![]() 得到
得到![]() =-1或
=-1或![]() =-4,从而得到m+n=0,或4m+n=0,进而得到4m2+5mn+n2=(4m+n)(m+n)=0正确;
=-4,从而得到m+n=0,或4m+n=0,进而得到4m2+5mn+n2=(4m+n)(m+n)=0正确;
C、由方程ax2+bx+c=0是倍根方程,得到x1=2x2,有已知条件得到得到抛物线的对称轴x=![]() ,可得x1和x2的值,可作判断.
,可得x1和x2的值,可作判断.
D、根据已知条件得到pq=2,解方程px2+3x+q=0得到方程的根;
x2+3x+2=0,
(x+1)(x+2)=0,
x1=-1,x2=-2,
∴方程x2+3x+2=0是倍根方程;
故A正确;
解方程(x-2)(mx+n)=0,
得:x1=2,x2=![]() ,
,
∵(x-2)(mx+n)=0是倍根方程,
∴![]() =-1或
=-1或![]() =-4,
=-4,
∴m+n=0或4m+n=0,
∵4m2+5mn+n2=(4m+n)(m+n)=0,
故B正确;
∵方程ax2+bx+c=0是倍根方程,
∴设x1=2x2,
∵相异两点M(1+t,s),N(4-t,s)都在抛物线y=ax2+bx+c上,
∴抛物线的对称轴x=![]() ,
,
∴x1+x2=5,
∴x2+2x2=5,
∴x1=![]() , x2=
, x2=![]()
故C不正确;
∵点(p,q)在反比例函数![]() 的图象上,
的图象上,
∴pq=2,
解方程px2+3x+q=0得:
x1=![]() ,x2=
,x2=![]() ,
,
∴x2=2x1,故D正确.
故选:C.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,一次函数
中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]()
![]() 的图象相交于
的图象相交于![]() ,
,![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() ,连接
,连接![]() ,且
,且![]() 的面积为2.
的面积为2.
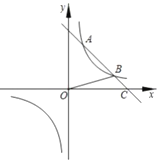
(1)求反比例函数的表达式;
(2)将直线![]() 向下平移,若平移后的直线与反比例函数的图象只有一个交点,试说明直线
向下平移,若平移后的直线与反比例函数的图象只有一个交点,试说明直线![]() 向下平移了几个单位长度?
向下平移了几个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中E为AD的中点,连接EC.
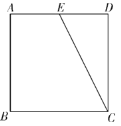
(1)作AEF∽DCE,点F在边AB上(要求:尺规作图,不写作法,保留作图痕迹):
(2)在(1)的条件下,连接CF,求证:AEF∽ECF.
查看答案和解析>>
科目:初中数学 来源: 题型:
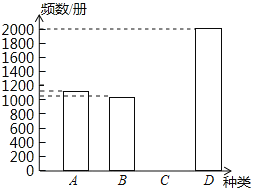
【题目】在学校开展的“献爱心”活动中,小东同学打算在暑假期间帮助一家社会福利书店推销A、B、C、D四种书刊.为了了解四种书刊的销售情况,小东对五月份这四种书刊的销售量进行了统计,小东通过采集数据,绘制了两幅不完整的统计图表(如图),请你根据所给出的信息解答以下问题:
书刊种类 | 频数 | 频率 |
A |
| 0.25 |
B | 1000 | 0.20 |
C | 750 | 0.15 |
D | 2000 |
|
(1)填充频率分布表中的空格及补全频数分布直方图;
(2)若该书店计划定购此四种书刊6000册,请你计算B种书刊应采购多少册较合适?
(3)针对调查结果,请你帮助小东同学给该书店提一条合理化的建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是某市2009年4月5日至14日每天最低气温的折线统计图.
(1)图2是该市2007年4月5日至14日每天最低气温的频数分布直方图,根据图1提供的信息,补全图2中频数分布直方图;
(2)在这10天中,最低气温的众数是____,中位数是____,方差是_____.
(3)请用扇形图表示出这十天里温度的分布情况.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,
中,![]() 为线段
为线段![]() 上的动点(不含端点
上的动点(不含端点![]() ),将
),将![]() 沿着
沿着![]() 翻折得到
翻折得到![]() ,
,
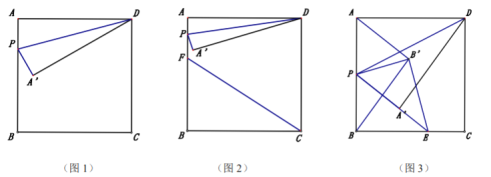
(1)如图1,当![]() ,求
,求![]() 长;
长;
(2)如图2,![]() 为线段
为线段![]() 上的点,当
上的点,当![]() 时,求点
时,求点![]() 由
由![]() 到
到![]() 的运动过程中,线段
的运动过程中,线段![]() 扫过的图形与
扫过的图形与![]() 重叠部分的面积;
重叠部分的面积;
(3)如图3,![]() 在
在![]() 上,连接
上,连接![]() ,将
,将![]() 沿着
沿着![]() 翻折得到
翻折得到![]() ,连结
,连结![]() ,问是否存在点
,问是否存在点![]() ,使得
,使得![]() 与
与![]() 相似?若存在,求出
相似?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司购买了一批![]() 、
、![]() 型芯片,其中
型芯片,其中![]() 型芯片的单价比
型芯片的单价比![]() 型芯片的单价少9元,已知该公司用3120元购买
型芯片的单价少9元,已知该公司用3120元购买![]() 型芯片的条数与用4200元购买
型芯片的条数与用4200元购买![]() 型芯片的条数相等.
型芯片的条数相等.
(1)求该公司购买的![]() 、
、![]() 型芯片的单价各是多少元?
型芯片的单价各是多少元?
(2)若两种芯片共购买了200条,且购买的总费用为6280元,求购买了多少条![]() 型芯片?
型芯片?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD的顶点A(0,﹣1),∠DAC=60°.若点P从点A出发,沿A→B→C→D→A…的方向,在菱形的边上以每秒0.5个单位长度的速度移动,则第2020秒时,点P的坐标为( )
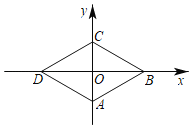
A.(2,0)B.(![]() ,0)C.(﹣
,0)C.(﹣![]() ,0)D.(0,1 )
,0)D.(0,1 )
查看答案和解析>>
科目:初中数学 来源: 题型:
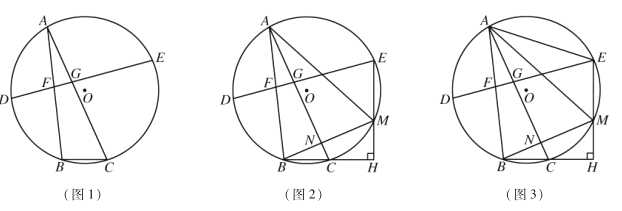
【题目】已知:![]() 是
是![]() 的内接三角形,点
的内接三角形,点![]() 为
为![]() 的中点,弦
的中点,弦![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,且
,且![]() .
.
(1)如图1,求证:![]() ;
;
(2)如图2,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,
,![]() 与
与![]() 的另一个交点为点
的另一个交点为点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,求证:
,求证:![]() ;
;
(3)如图3,在(2)的条件下,连接![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com