Question

【题目】图1是某市2009年4月5日至14日每天最低气温的折线统计图．

（1）图2是该市2007年4月5日至14日每天最低气温的频数分布直方图，根据图1提供的信息，补全图2中频数分布直方图；

（2）在这10天中，最低气温的众数是____，中位数是____，方差是_____．

（3）请用扇形图表示出这十天里温度的分布情况．

Answer 1

【答案】(1)作图见解析；（2）7，7.5，2.8；（3）见解析.

【解析】

（1）根据图1找出8、9、10℃的天数，然后补全统计图即可；

（2）根据众数的定义，找出出现频率最高的温度；按照从低到高排列，求出第5、6两个温度的平均数即为中位数；先求出平均数，再根据方差的定义列式进行计算即可得解；

（3）求出7、8、9、10、11℃的天数在扇形统计图中所占的度数，然后作出扇形统计图即可．

（1）由图1可知，8℃有2天，9℃有0天，10℃有2天，

补全统计图如图；

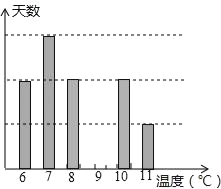
（2）根据条形统计图，7℃出现的频率最高，为3天，

所以，众数是7；

按照温度从小到大的顺序排列，第5个温度为7℃，第6个温度为8℃，

所以，中位数为（7+8）=7.5；

平均数为（6×2+7×3+8×2+10×2+11）=×80=8，

所以，方差=[2×（6﹣8）2+3×（7﹣8）2+2×（8﹣8）2+2×（10﹣8）2+（11﹣8）2]，

=（8+3+0+8+9），

=×28，

=2.8；

（3）6℃的度数，×360°=72°，

7℃的度数，×360°=108°，

8℃的度数，×360°=72°，

10℃的度数，×360°=72°，

11℃的度数，×360°=36°，

作出扇形统计图如图所示．