
【题目】在平面直角坐标系中,我们把横、纵坐标均为整数的点叫做整点.已知反比例函数y=![]() (m<0)与y=x2﹣4在第四象限内围成的封闭图形(包括边界)内的整点的个数为2,则实数m的取值范围为__.
(m<0)与y=x2﹣4在第四象限内围成的封闭图形(包括边界)内的整点的个数为2,则实数m的取值范围为__.
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD⊥BC于D,E是AD上一点,BE的延长线交AC于F,若BD=AD,DE=DC.

(1)求证BF⊥AC;
(2)若AE=2,BE=4,AF=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,记∠ABC=∠α(0°<∠α<90°),菱形的面积记作S,菱形的周长记作C,若AD=2,则( )
A. C与∠α的大小有关
B. 当∠α=45°时,S=![]()
C. A,B,C,D四个点可以在同一个圆上
D. S随∠α的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为![]() ,连接AC、BD交于点O,CE平分∠ACD交BD于点E,
,连接AC、BD交于点O,CE平分∠ACD交BD于点E,
(1)求DE的长;
(2)过点EF作EF⊥CE,交AB于点F,求BF的长;
(3)过点E作EG⊥CE,交CD于点G,求DG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,∠CAB=90°,AC=AB=3,△CDE中,∠CDE=90°,CD=DE=5,连接BE,取BE中点F,连接AF、DF.

(1)如图1,若C、B、E三点共线,H为BC中点.
①直接指出AF与DF的关系 ;
②直接指出FH的长度 ;
(2)将图(1)中的△CDE绕C点逆时针旋转a(如图2,0°<α<180°),试确定AF与DF的关系,并说明理由;
(3)在(2)中,若AF=![]() ,请直接指出点F所经历的路径长.
,请直接指出点F所经历的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,⊙O的半径为4,点A是⊙O上一点,直线l过点A;P是⊙O上的一个动点(不与点A重合),过点P作PB⊥l于点B,交⊙O于点E,直径PD延长线交直线l于点F,点A是![]() 的中点.
的中点.
(1)求证:直线l是⊙O的切线;
(2)若PA=6,求PB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是某市2009年4月5日至14日每天最低气温的折线统计图.
(1)图2是该市2007年4月5日至14日每天最低气温的频数分布直方图,根据图1提供的信息,补全图2中频数分布直方图;
(2)在这10天中,最低气温的众数是____,中位数是____,方差是_____.
(3)请用扇形图表示出这十天里温度的分布情况.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知动点A在函数y=![]() (x>0)的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC,直线DE分别交x轴,y轴于点P,Q,当QE:DP=9:25时,图中的阴影部分的面积等于___.
(x>0)的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC,直线DE分别交x轴,y轴于点P,Q,当QE:DP=9:25时,图中的阴影部分的面积等于___.

查看答案和解析>>
科目:初中数学 来源: 题型:
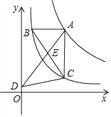
【题目】如图,点A是反比例函数y=![]() 图象上的任意一点,过点A作AB∥x轴,AC∥y轴,分别交反比例函数y=
图象上的任意一点,过点A作AB∥x轴,AC∥y轴,分别交反比例函数y=![]() 的图象于点B,C,连接BC,E是BC上一点,连接并延长AE交y轴于点D,连接CD,则S△DEC﹣S△BEA=_________.
的图象于点B,C,连接BC,E是BC上一点,连接并延长AE交y轴于点D,连接CD,则S△DEC﹣S△BEA=_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com