【题目】如图，BD是△ABC的角平分线，过点D作DE∥BC交AB于点E，DF∥AB交BC于点F．

（1）求证：四边形BEDF为菱形；

（2）如果∠A=90°，∠C=30°，BD=12，求菱形BEDF的面积．

参考答案：

【答案】(1)见解析;(2)24.

【解析】

（1）根据平行四边形的和菱形的判定证明即可；

（2）根据含30°的直角三角形的性质和勾股定理以及菱形的面积解答即可．

证明：（1）∵DE∥BC，DF∥AB，

∴四边形BFDE是平行四边形，

∵BD是△ABC的角平分线，

∴∠EBD=∠DBF，

∵DE∥BC，

∴∠EDB=∠DBF，

∴∠EBD=∠EDB，

∴BE=ED，

∴平行四边形BFDE是菱形；

（2）连接EF，交BD于O，

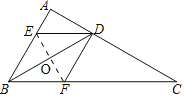
∵∠BAC=90°，∠C=30°，

∴∠ABC=60°，

∵BD平分∠ABC，

∴∠DBC=30°，

∴BD=DC=12，

∵DF∥AB，

∴∠FDC=∠A=90°，

∴DF=，

在Rt△DOF中，OF=，

∴菱形BFDE的面积=×EFBD＝×12×4=24．

关闭