
【题目】已知二次函数![]() 的图象如图所示,它与
的图象如图所示,它与![]() 轴的两个交点分别为
轴的两个交点分别为![]() ,
,![]() .对于下列命题:①
.对于下列命题:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的有( )
.其中正确的有( )

A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
【答案】B
【解析】
首先根据图象可得:抛物线开口向上,则a>0.抛物线与y交与负半轴,则c<0,对称轴:![]() 结合图象与x轴的交点可得对称轴为x=1,结合对称轴公式可判断出①的正误;根据对称轴公式结合a的取值可判定出b<0,根据a、b、c的正负即可判断出②的正误;利用a-b+c=0,求出a-2b+4c<0,即可判断出③的正误;利用当x=4时,y>0,则16a+4b+c>0,由①知,b=-2a,得出8a+c>0,即可判断出④的正误.
结合图象与x轴的交点可得对称轴为x=1,结合对称轴公式可判断出①的正误;根据对称轴公式结合a的取值可判定出b<0,根据a、b、c的正负即可判断出②的正误;利用a-b+c=0,求出a-2b+4c<0,即可判断出③的正误;利用当x=4时,y>0,则16a+4b+c>0,由①知,b=-2a,得出8a+c>0,即可判断出④的正误.
根据图象可得:抛物线开口向上,则a>0.抛物线与y交与负半轴,则c<0,
对称轴:![]()
①∵它与x轴的两个交点分别为(1,0),(3,0),
∴对称轴是x=1,
∴![]()
∴b+2a=0,
故①错误;
②∵a>0,
∴b<0,
∵c<0,
∴abc>0,故②错误;
③∵ab+c=0,
∴c=ba,
∴a2b+4c=a2b+4(ba)=2b3a,
又由①得b=2a,
∴a2b+4c=7a<0,
故③正确;
④根据图示知,当x=4时,y>0,
∴16a+4b+c>0,
由①知,b=2a,
∴8a+c>0;
故④正确;
综上所述,正确的结论是:③④,
故选:B.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:
【题目】![]() 在方格中的位置如图所示.
在方格中的位置如图所示.
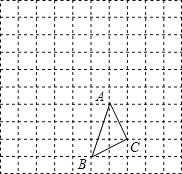
(1)请在方格纸上(小方格的边长为1)建立平面直角坐标系,使得A、B两点的坐标分别为![]() ,
,![]() .并求出C点的坐标;
.并求出C点的坐标;
(2)作出![]() 关于x轴对称的
关于x轴对称的![]() ,并写出
,并写出![]() 、
、![]() 两点的坐标.
两点的坐标.
(3)求![]() 的面积。
的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是△ABC的角平分线,过点D作DE∥BC交AB于点E,DF∥AB交BC于点F.
(1)求证:四边形BEDF为菱形;
(2)如果∠A=90°,∠C=30°,BD=12,求菱形BEDF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个二次函数的图象,三位同学分别说出了它的一些特点:
甲:对称轴为直线x=4
乙:与x轴两个交点的横坐标都是整数.
丙:与y轴交点的纵坐标也是整数,且以这三个点为顶点的三角形面积为3.请你写出满足上述全部特点的一个二次函数解析式__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 上部分点的横坐标
上部分点的横坐标![]() ,纵坐标
,纵坐标![]() 的对应值如下表:
的对应值如下表:
| … |
|
|
|
|
| … |
| … |
|
|
|
|
| … |
![]() 根据上表填空:
根据上表填空:
①抛物线与![]() 轴的交点坐标是________和________;
轴的交点坐标是________和________;
②抛物线经过点![]() ,________
,________![]() ;
;
③在对称轴右侧,![]() 随
随![]() 增大而________;
增大而________;
![]() 试确定抛物线
试确定抛物线![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,E、F分别是AB、BC边的中点,EP⊥CD于点P,∠BAD=110°,则∠FPC的度数是( )

A. 35° B. 45° C. 50° D. 55°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中有三个点A(-3,2)、B(-4,-3)、C(-1,-1)
(1)连接A、B、C三点,请在右图中作出△ABC关于x轴对称的图形△A/B/C/,并直接写出对称点A/,B/,C/的坐标;
(2)用直尺在纵轴上找到一点P(0,n)满足PB/+PA的值最小(在图中标明点P的位置,并写出n的值在哪两个连续整数之间).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com