
【题目】如图,在矩形纸片ABCD中,点P在边AB上,沿着PC折叠纸片使B点落在边AD上的E点处,过点E作EF∥AB交PC于F,连接BF.
(1)求证:四边形BFEP为菱形;
(2)若tan∠BCP=![]() ,AB=3cm,求AE的长.
,AB=3cm,求AE的长.

【答案】(1)详见解析;(2)AE=1 cm.
【解析】
(1)由折叠的性质得出PB=PE,BF=EF,∠BPF=∠EPF,由平行线的性质得出∠BPF=∠EFP,证出∠EPF=∠EFP,得出EP=EF,所以BP=BF=EF=EP,即可得出结论;(2)由折叠可知,∠BCP=∠ECP,根据已知可得tan∠ECP =tan∠BCP=![]() ,根据锐角三角函数的定义可得
,根据锐角三角函数的定义可得![]() ,再证明△APE∽△DEC,根据相似三角形的性质可得
,再证明△APE∽△DEC,根据相似三角形的性质可得![]() .再由AB=DC=3cm,即可求得AE=1 cm.
.再由AB=DC=3cm,即可求得AE=1 cm.
(1)证明:∵折叠纸片使B点落在边AD上的E处,折痕为PC,
∴B点与E点关于PQ对称.
∴BP=PE,BF=FE,∠BPF=∠EPF.
又∵EF∥AB,
∴∠BPF=∠EFP.
∴∠EPF=∠EFP.
∴EP=EF.
∴BP=BF=FE=EP.
∴四边形BFEP为菱形.
(2)由折叠可知,∠BCP=∠ECP.
∴![]() .
.
∴![]() ,
,
∵∠PEC=∠A=∠D=90°.
∴∠AEP+∠DEC=90°,∠AEP+∠APE=90°.
∴∠APE=∠DEC.
∴△APE∽△DEC.
∴![]() .
.
∵AB=DC=3cm,
∴AE=1 cm.


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知△ABE与△CDE都是等腰直角三角形,∠AEB=∠DEC=90°,连接AD,AC,BC,BD,若AD=AC=AB,则下列结论:①AE垂直平分CD,②AC平分∠BAD,③△ABD是等边三角形,④∠BCD的度数为150°,其中正确的个数是( )

A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 在方格中的位置如图所示.
在方格中的位置如图所示.
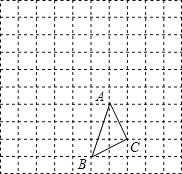
(1)请在方格纸上(小方格的边长为1)建立平面直角坐标系,使得A、B两点的坐标分别为![]() ,
,![]() .并求出C点的坐标;
.并求出C点的坐标;
(2)作出![]() 关于x轴对称的
关于x轴对称的![]() ,并写出
,并写出![]() 、
、![]() 两点的坐标.
两点的坐标.
(3)求![]() 的面积。
的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直角三角形纸片ABC中,∠ACB=90°,AC≤BC,如图,将纸片沿某条直线折叠,使点A落在直角边BC上,记落点为D,设折痕与AB、AC边分别交于点E、F.
(1)如果∠AFE=65°,求∠CDF的度数;
(2)若折叠后的△CDF与△BDE均为等腰三角形,那么纸片中∠B的度数是多少?写出你的计算过程,并画出符合条件的折叠后的图形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读对学生的成长有着深远的影响,某中学为了解学生每周课余阅读的时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表.
组别 | 时间(小时) | 频数(人数) | 频率 |
A | 0≤t≤0.5 | 6 | 0.15 |
B | 0.5≤t≤1 | a | 0.3 |
C | 1≤t≤1.5 | 10 | 0.25 |
D | 1.5≤t≤2 | 8 | b |
E | 2≤t≤2.5 | 4 | 0.1 |
合计 | 1 |
请根据图表中的信息,解答下列问题:
(1)表中的a= ,b= ,中位数落在 组,将频数分布直方图补全;
(2)估计该校2000名学生中,每周课余阅读时间不足0.5小时的学生大约有多少名?
(3)E组的4人中,有1名男生和3名女生,该校计划在E组学生中随机选出两人向全校同学作读书心得报告,请用画树状图或列表法求抽取的两名学生刚好是1名男生和1名女生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
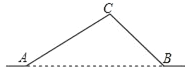
【题目】如图,从A地到B地的公路需要经过C地,根据规划,将在A,B两地之间修建一条笔直的公路.已知AC=10千米,∠CAB=34°,∠CBA=45°,求改直后公路AB的长(结果精确到0.1千米)
(参考数据:sin34°≈0.559,cos34°≈0.829,tan34°≈0.675)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是△ABC的角平分线,过点D作DE∥BC交AB于点E,DF∥AB交BC于点F.
(1)求证:四边形BEDF为菱形;
(2)如果∠A=90°,∠C=30°,BD=12,求菱形BEDF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,E、F分别是AB、BC边的中点,EP⊥CD于点P,∠BAD=110°,则∠FPC的度数是( )

A. 35° B. 45° C. 50° D. 55°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com