
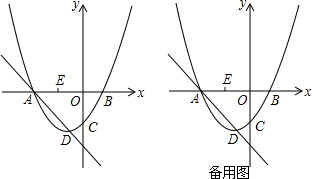
���� ��1��ֻ����y=0�Ϳ������A��B�����꣬�������ߵĽ���ʽ��ɶ���ʽ�Ϳɵõ�����D�����꣬��������AE��EB=1��2�Ϳ������E�����ꣻ
��2����Ȼ����ת���ֱ����ʹ�á�MEB=90��͡�EBM=90��ĵ�M����һ����Ҫʹ���������ĵ�M����ֻ��������ֻ����ת���ֱ����ʹ�á�EMB=90��ĵ�Mֻ��һ�������ڵ�M����BEΪֱ���ġ�O�ϣ������ת���ֱ�����Oֻ��һ�����㣬����ֱ�����O������M����OM��AM����ͼ1��ͼ2��ֻ���������Ǻ��������OAM���Ϳɽ�����⣻
��3����ֱ��AP��y�ύ�ڵ�Q������Q��QH��AC��H����ͼ3��ͨ�����ACQ�Ϳ����QC���Ӷ��õ���Q�����꣬Ҫ���P������ֻ�����ֱ��AP�Ľ���ʽ�����ڵ�A��Q��������֪��ֻ�����ô���ϵ�����Ϳɽ�����⣮
��� �⣺��1����y=0����$\frac{1}{3}$x2+$\frac{2}{3}$x-$\frac{8}{3}$=0��
���x1=-4��x2=2��
��A��-4��0����B��2��0����
��AB=2-��-4��=6��OA=4��
��y=$\frac{1}{3}$x2+$\frac{2}{3}$x-$\frac{8}{3}$=$\frac{1}{3}��x+1��^{2}-3$��D��-1��-3����
��AE��EB=1��2��
��AE=$\frac{1}{3}AB$=2��
��OE=2��
��E��-2��0����
��2����Ȼ����ת���ֱ����ʹ�á�MEB=90��͡�EBM=90��ĵ�M����һ����
Ҫʹ���������ĵ�M����ֻ��������ֻ����ת���ֱ����ʹ�á�EMB=90��ĵ�Mֻ��һ����
���ڵ�M����BEΪֱ���ġ�O�ϣ������ת���ֱ�����Oֻ��һ�����㣬
����ֱ�����O������M����OM��AM����ͼ1��ͼ2��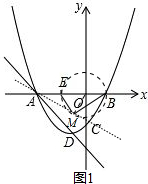
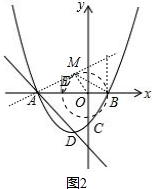
��Rt��AMO��sin��OAM=$\frac{OM}{OA}$=$\frac{2}{4}$=$\frac{1}{2}$��
���OAM=30�㣮
��tan��OAD=$\frac{3}{-1-��-4��}$=1��
���OAD=45�㣬
��t1=$\frac{45-30}{5}$=3��t2=$\frac{45+30}{5}$=15��
����תʱ��Ϊ3���15�룻
��3����ֱ��AP��y�ύ�ڵ�Q������Q��QH��AC��H����ͼ3��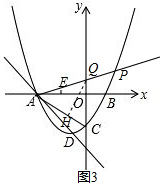
���С�PAC=45�㣬C��0��-$\frac{8}{3}$����OC=$\frac{8}{3}$��
��tan��ACO=$\frac{4}{\frac{8}{3}}$=$\frac{3}{2}$��AC=$\sqrt{{4}^{2}+��\frac{8}{3}��^{2}}$=$\frac{4\sqrt{13}}{3}$��
��HC=2x����tan��HCQ=$\frac{QH}{CH}$=$\frac{3}{2}$��QH=3x��
��tan��QAH=$\frac{QH}{AH}$=1��AH=QH=3x��
��AC=3x+2x=5x=$\frac{4\sqrt{13}}{3}$��
��x=$\frac{4\sqrt{13}}{15}$��
��QC=$\sqrt{H{C}^{2}+Q{H}^{2}}$=$\sqrt{��2x��^{2}+��3x��^{2}}$=$\sqrt{13}$x=$\frac{52}{15}$��
��OQ=$\frac{52}{15}$-$\frac{8}{3}$=$\frac{12}{15}$=$\frac{4}{5}$��
��Q��0��$\frac{4}{5}$����
��ֱ��AP�Ľ���ʽΪy=kx+b��
����$\left\{\begin{array}{l}{-4k+b=0}\\{b=\frac{4}{5}}\end{array}\right.$
���$\left\{\begin{array}{l}{k=\frac{1}{5}}\\{b=\frac{4}{5}}\end{array}\right.$
��ֱ��AP�Ľ���ʽΪy=$\frac{1}{5}$x+$\frac{4}{5}$��
�ⷽ����$\left\{\begin{array}{l}{y=\frac{1}{5}x+\frac{4}{5}}\\{y=\frac{1}{3}{x}^{2}+\frac{2}{3}x-\frac{8}{3}}\end{array}\right.$��$\left\{\begin{array}{l}{{x}_{1}=-4}\\{{y}_{1}=0}\end{array}\right.$��$\left\{\begin{array}{l}{{x}_{2}=\frac{13}{5}}\\{{y}_{2}=\frac{33}{25}}\end{array}\right.$
���P��������$\frac{13}{5}$��$\frac{33}{25}$����
���� ������Ҫ���������ô���ϵ������ֱ�ߵĽ���ʽ���������ϵ������������ֱ���������ߵĽ������⡢���Ǻ��������ɶ�����Բ�ܽǶ�����ֱ����Բ���е�֪ʶ���ۺ��ԱȽ�ǿ���ѶȱȽϴ�����ת��Ϊֱ����Բ��λ�ù�ϵ�ǽ���ڣ�2��С��Ĺؼ���ͨ�����ACQ���QC�ǽ���ڣ�3��С��Ĺؼ���


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017�콭��ʡ�߰��о��꼶��ѧ�ڵ�һ��ģ�⿼����ѧ�Ծ��������棩 ���ͣ��ж���
�ס��ҡ����������˲μ�ijУ��Ƹ��ʦ���ԣ��Ժ�ס�������ȥѯ�ʳɼ��������������ش��߶Լס������˻ش�����ݽ��з���:
��1���оٳ������˵������������п��ܳ��ֵIJ�ͬ���
��2��������ڵ�һ���ĸ��ʣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ��ұ�о��꼶3���п�ģ����ѧ�Ծ��������棩 ���ͣ��ж���
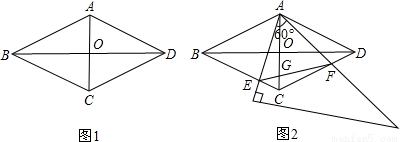
��ͼ1��������ABCD�У�AC=2��BD=2 ��AC��BD�ཻ�ڵ�O��
��AC��BD�ཻ�ڵ�O��
��1�����AB�ij���
��2����ͼ2����һ���㹻���ֱ�����ǰ�60��ǵĶ����������ABCD�Ķ���A�����Ƶ�A������ת���������ǰ�60��ǵ����߷ֱ����BC��CD�ཻ�ڵ�E��F������EF��AC�ཻ�ڵ�G��
���жϡ�AEF����һ�����������Σ���˵�����ɣ�
����ת�����У�����EΪ��BC���ĵȷֵ�ʱ��BE��CE������CG�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ��ұ�о��꼶3���п�ģ����ѧ�Ծ��������棩 ���ͣ���ѡ��
��ͼ��ʾ�ļ�����ĸ���ͼ�ǣ� ��
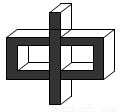
A.  B.
B.  C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
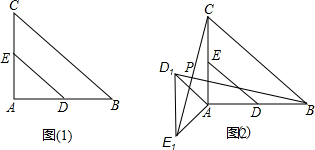 ��ͼ��1������Rt��ABC�У���A=90�㣬AC=AB=4��D��E�ֱ���AB��AC���е㣮������Rt��ADE�Ƶ�A��ʱ����ת���õ�����Rt��AD1E1����ͼ��2��������ת��Ϊ����0������180�㣩����ֱ��BD1��CE1�Ľ���ΪP��
��ͼ��1������Rt��ABC�У���A=90�㣬AC=AB=4��D��E�ֱ���AB��AC���е㣮������Rt��ADE�Ƶ�A��ʱ����ת���õ�����Rt��AD1E1����ͼ��2��������ת��Ϊ����0������180�㣩����ֱ��BD1��CE1�Ľ���ΪP���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com