
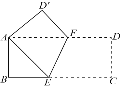
【题目】如图,将矩形ABCD沿EF折叠,点C落在A处,点D落在![]() 处.若AB=3,BC=9,则折痕EF的长为()
处.若AB=3,BC=9,则折痕EF的长为()
A. ![]() B. 4 C. 5 D.
B. 4 C. 5 D. ![]()
【答案】A
【解析】
根据翻折的性质可得AE=EC,∠AEF=∠CEF,设AE=x,表示出BE.在Rt△ABE中,利用勾股定理列方程求出x,根据两直线平行,内错角相等可得∠AFE=∠CEF,从而得到∠AEF=∠AFE,根据等角对等边可得AF=AE,过点E作EG⊥AD于G,求出AG、GF,再利用勾股定理列式计算即可得解.
∵矩形ABCD沿EF折叠,点C落在A处,∴AE=EC,∠AEF=∠CEF,
设AE=x,则BE=BC﹣EC=9﹣x,
在Rt△ABE中,根据勾股定理得:AB2+BE2=AE2,
即32+(9﹣x)2=x2,
解得:x=5,
所以,AE=5,BE=9﹣5=4,
∵矩形对边AD∥BC,∴∠AFE=∠CEF,∴∠AEF=∠AFE,∴AF=AE=5,
过点E作EG⊥AD于G,则四边形ABEG是矩形,∴AG=BE=4,
GF=AF﹣AG=5﹣4=1,
在Rt△EFG中,根据勾股定理得:EF=![]() =
=![]() =
=![]() .
.
故选A.


科目:初中数学 来源: 题型:
【题目】近年来,随着我国的科学技术的迅猛发展,很多行业已经由“中国制造”升级为“中国创造”,高铁事业是“中国创造”的典范,一般的高铁包括G字头的高速动车组以及D字头的动车组.由大连到北京的G377的平均速度是D31的平均速度的1.2倍,行驶相同的路程1500千米,G377少用1个小时.
(1)求D31的平均速度.
(2)若以“速度与票价的比值”定义这两种列车的性价比,人们出行都喜欢选择性价比高的方式.现阶段D31票价为266元/张,G377票价为400元/张,如果你有机会给有关部门提一个合理化建议,使G377的性价比达到D31的性价比,你如何建议,为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a是最大的负整数,b、c满足(b﹣3)2+|c+4|=0,且a,b,c分别是点A,B,C在数轴上对应的数.
![]()
(1)求a,b,c的值,并在数轴上标出点A,B,C;
(2)若动点P从C出发沿数轴正方向运动,点P的速度是每秒2个单位长度,运动几秒后,点P到达B点?
(3)在数轴上找一点M,使点M到A,B,C三点的距离之和等于13,请直接写出所有点M对应的数.(不必说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有 20 筐白菜,以每筐 25 千克为标准,超过或不足的分别用正、负来表示,记录如下:

(1)与标准质量比较,20 筐白菜总计超过或不足多少千克?
(2)若白菜每千克售价 2 .6 元,则出售这 20 筐白菜可卖多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,在△ABC中,以AB、AC为直角边, 分别向外作等腰直角三角形ABE、ACF,连结EF,过点A作AD⊥BC,垂足为D,反向延长DA交EF于点M.
(1)用圆规比较EM与FM的大小.
(2)你能说明由(1)中所得结论的道理吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
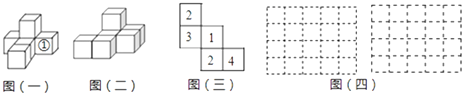
【题目】按要求完成问题:(1)如图(一),它是由6个同样大小的正方体摆成的几何体.将正方体①移走后,新几何体的三视图与原几何体的三视图相比,哪一个视图没有发生改变?
(2)如图(二),请你借助图四虚线网格画出该几何体的俯视图.
(3)如图(三),它是由几个小立方块组成的俯视图,小正方形上的数字表示该位置上的正方体的个数,请你借助图四虚线网格画出该几何体的主视图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,不正确的是![]()
![]()
![]() 全等形的面积相等;
全等形的面积相等;
![]() 形状相同的两个三角形是全等三角形;
形状相同的两个三角形是全等三角形;
![]() 全等三角形的对应边,对应角相等;
全等三角形的对应边,对应角相等;
![]() 若两个三角形全等,则其中一个三角形一定是由另一个三角形旋转得到的.
若两个三角形全等,则其中一个三角形一定是由另一个三角形旋转得到的.
A. ![]() 与
与![]() B.
B. ![]() 与
与![]() C.
C. ![]() 与
与![]() D.
D. ![]() 与
与![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,点O在AB上,经过点A的⊙O与BC相切于点D,与AC,AB分别相交于点E,F,连接AD与EF相交于点G.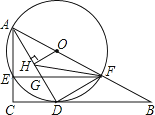
(1)求证:AD平分∠CAB;
(2)若OH⊥AD于点H,FH平分∠AFE,DG=1.
①试判断DF与DH的数量关系,并说明理由;
②求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC经过一次平移到△DFE的位置,请回答下列问题:

(1)点C的对应点是点__________,∠D=__________,BC=__________;
(2)连接CE,那么平移的方向就是__________的方向,平移的距离就是线段__________的长度;
(3)连接AD,BF,BE,与线段CE相等的线段有__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com