Question

【题目】已知如图,在△ABC中,以AB、AC为直角边, 分别向外作等腰直角三角形ABE、ACF,连结EF,过点A作AD⊥BC,垂足为D,反向延长DA交EF于点M.

(1)用圆规比较EM与FM的大小.

(2)你能说明由(1)中所得结论的道理吗?

Answer 1

【答案】(1)EM=FM；（2）证明见解析.

【解析】

(1)直接用圆规比较两线段的大小；（2）作EH⊥AM,垂足为H,FK⊥AM,垂足为K.先说明Rt△EHA≌Rt△ADB, 得EH=AD,Rt△FKA≌Rt△ADC, 得FK=AD,得EH=FK,在Rt△EHK与Rt△FKM中,Rt△EHM≌Rt△FKM,得EM=FM.

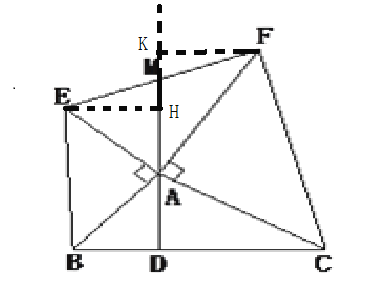
解：(1)EM=FM

(2)作EH⊥AM,垂足为H,FK⊥AM,垂足为K,则∠AHE=90,∠AKF=90,

因为，AD⊥BC,

所以，∠ADB=90,

所以，∠ABD+∠BAD=90,

又因为，△ABE是等腰直角三角形，

所以，AE=AB,∠BAE=90,

所以，∠EAH+∠BAD=90,

所以，∠EAH=∠ABD，

所以，Rt△EHA≌Rt△ADB（AAS），

所以，EH=AD，

同理：

Rt△FKA≌Rt△ADC， FK=AD，

所以EH=FK

在Rt△EHK与Rt△FKM中,

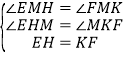
所以，Rt△EHM≌Rt△FKM（AAS）

得EM=FM.