
【题目】如图,在四边形ABCD中,AD∥BC,若∠DAB的角平分线AE交CD于E,连接BE,且BE边平分∠ABC,则以下命题不正确的个数是①BC+AD=AB;②E为CD中点;③∠AEB=90°;④S△ABE=![]() S四边形ABCD;⑤BC=CE.( )
S四边形ABCD;⑤BC=CE.( )

A. 0个 B. 1个 C. 2个 D. 3个
【答案】B
【解析】
试题∵AD∥BC,
∴∠ABC+∠BAD=180°,
∵AE、BE分别是∠BAD与∠ABC的平分线,
∴∠BAE=![]() ∠BAD,∠ABE=
∠BAD,∠ABE=![]() ∠ABC,
∠ABC,
∴∠BAE+∠ABE=![]() (∠BAD+∠ABC)=90°,
(∠BAD+∠ABC)=90°,
∴∠AEB=180°-(∠BAE+∠ABE)=180°-90°=90°,
故③小题正确;
延长AE交BC延长线于F,

∵∠AEB=90°,
∴BE⊥AF,
∵BE平分∠ABC,
∴∠ABE=∠FBE,
在△ABE与△FBE中,
 ,
,
∴△ABE≌△FBE(ASA),
∴AB=BF,AE=FE,
∵AD∥BC,
∴∠EAD=∠F,
在△ADE与△FCE中,
 ,
,
∴△ADE≌△FCE(ASA),
∴AD=CF,
∴AB=BC+CF=BC+AD,故①小题正确;
∵△ADE≌△FCE,
∴CE=DE,即点E为CD的中点,故②小题正确;
∵△ADE≌△FCE,
∴S△ADE=S△FCE,
∴S四边形ABCD=S△ABF,
∵S△ABE=![]() S△ABE,
S△ABE,
∴S△ABE=![]() S四边形ABCD,故④小题正确;
S四边形ABCD,故④小题正确;
若AD=BC,则CE是Rt△BEF斜边上的中线,则BC=CE,
∵BD与BC不一定相等,
∴BC与CE不一定相等,故⑤小题错误.
综上所述,不正确的有⑤共1个.
故选B.


科目:初中数学 来源: 题型:
【题目】已知如图,在△ABC中,以AB、AC为直角边, 分别向外作等腰直角三角形ABE、ACF,连结EF,过点A作AD⊥BC,垂足为D,反向延长DA交EF于点M.
(1)用圆规比较EM与FM的大小.
(2)你能说明由(1)中所得结论的道理吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段 AB=24,动点 P 从 A 出发,以每秒 2 个单位的速度沿射线 AB运动,运动时间为 t 秒(t>0),M 为 AP 的中点.
(1)当点 P 在线段 AB 上运动时,
①当 t 为多少时,PB=2AM?②求2BM-BP的值.
(2)当 P 在 AB 延长线上运动时,N 为 BP 的中点,说明线段 MN 的长度不变,并 求出其值.
(3)在 P 点的运动过程中,是否存在这样的 t 的值,使 M、N、B 三点中的一个点 是以其余两点为端点的线段的中点,若有,请求出 t 的值;若没有,请说明理 由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8 分)2013 年 4 月起泉州市区居民生活用水开始实行阶梯式计量水价,据了解,此次实行的阶梯式计量水价分为三级(如表所示):

例:若某用户 2013 年 6 月份的用水量为 35 吨,按三级计算则应交水费为:
20×1.65+(30﹣20)×2.48+(35﹣30)×3.30=74.3(元)
(1)如果小东家 2013 年 6 月份的用水量为 20 吨,则需缴交水费多少元?
(2)如果小明家 2013 年 7 月份的用水量为 a 吨,水价要按两级计算,则小明家该月应缴交水费多少元?(用含 a 的代数式表示,并化简)
(3)若一用户 2013 年 7 月份应该水费 90.8 元,则该户人家 7 月份用水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】襄阳市某企业积极响应政府“创新发展”的号召,研发了一种新产品.已知研发、生产这种产品的成本为30元/件,且年销售量y(万件)关于售价x(元/件)的函数解析式为:y= ![]() .
.
(1)若企业销售该产品获得的年利润为W(万元),请直接写出年利润W(万元)关于售价x(元/件)的函数解析式;
(2)当该产品的售价x(元/件)为多少时,企业销售该产品获得的年利润最大?最大年利润是多少?
(3)若企业销售该产品的年利润不少于750万元,试确定该产品的售价x(元/件)的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC经过一次平移到△DFE的位置,请回答下列问题:

(1)点C的对应点是点__________,∠D=__________,BC=__________;
(2)连接CE,那么平移的方向就是__________的方向,平移的距离就是线段__________的长度;
(3)连接AD,BF,BE,与线段CE相等的线段有__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某运算程序,该程序是循环迭代的一种.根据该程序的指令,如果输入![]() 的值是10,那么得到第1次输出的值是5;把第1次输出的值再次输入,那么第2次输出的值是6;把第2次输出的值再次输入,那么第3次输出的值是3;…,第2018次输出的值是( )
的值是10,那么得到第1次输出的值是5;把第1次输出的值再次输入,那么第2次输出的值是6;把第2次输出的值再次输入,那么第3次输出的值是3;…,第2018次输出的值是( )

A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在综合实践课上,小聪所在小组要测量一条河的宽度,如图,河岸EF∥MN,小聪在河岸MN上点A处用测角仪测得河对岸小树C位于东北方向,然后沿河岸走了30米,到达B处,测得河对岸电线杆D位于北偏东30°方向,此时,其他同学测得CD=10米.请根据这些数据求出河的宽度为米.(结果保留根号)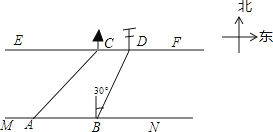
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)![]() = ___________;(2)
= ___________;(2)![]() =___________;(3)
=___________;(3)![]() =___________;(4)
=___________;(4)![]() =________;(5)
=________;(5)![]() __________;(6)
__________;(6)![]() =___;(7)
=___;(7)![]() _____;(8)
_____;(8)![]() =__________.
=__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com