
【题目】(感知)“如图①,![]() ,
,![]() 平分
平分![]() ,作
,作![]() ,
,![]() 、
、![]() 分别交射线
分别交射线![]() 、
、![]() 于
于![]() 、
、![]() 两点,连结
两点,连结![]() ,求
,求![]() 的度数”为了求解问题,某同学做了如下的分析,
的度数”为了求解问题,某同学做了如下的分析,
“过点![]() 作
作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,”进而求解,则
,”进而求解,则![]() ________
________![]() .
.
(拓展)如图②,一般地,设![]()
![]() ,
,![]() 平分
平分![]() ,作
,作![]() ,
,![]() 、
、![]() 分别交射线
分别交射线![]() 、
、![]() 于
于![]() 、
、![]() 两点,连结
两点,连结![]() .
.
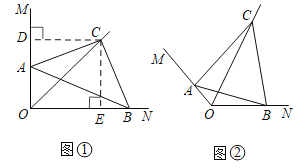
(1)求![]() 的度数.(用含
的度数.(用含![]() 的代数式表示)
的代数式表示)
(2)若![]() ,
,![]() ,
,![]() ,则
,则![]() ________.
________.
【答案】45;(1)![]() ;(2)
;(2)![]() .
.
【解析】
先证明四边形ODCE是矩形,得∠DCA=∠BCE,再证明△CAD≌△CBE(ASA),得AC=BC,进而可求得∠ABC;
(1)过点C作CD⊥OM于点D,CE⊥ON于点E,证明△ACD≌△BCE(ASA),即可求得∠ABC;
(2)过点C作CD⊥OM于点D,CE⊥ON于点E,证明△ACD≌△BCE(ASA),△OCD≌△OCE(HL),可求得OD=OE=5,再利用特殊角三角函数值即可.
解:【感知】如图①,∵CD⊥OM,CE⊥ON,

∴∠CDO=∠CEO=∠MON=90°,
∴四边形ODCE是矩形,
∴∠DCE=∠ACB=90°,
∴∠DCA+∠ACE=∠BCE+∠ACE,
∴∠DCA=∠BCE,
∵OC平分∠MON,
∴CD=CE,
∴△CAD≌△CBE(ASA),
∴AC=BC,
∴∠CAB=∠CBA,
∵∠CAB+∠CBA=90°,
∴∠CAB=∠CBA=45,°
故答案为:45°;
【拓展】
(1)如图②,过点C作CD⊥OM于点D,CE⊥ON于点E,
∴∠ADC=∠BEC=90°,
∵OC平分∠MON,
∴CD=CE,
∵∠DCE=180°﹣α,∠ACB=180°﹣α,
∴∠DCE=∠ACB,
∴∠DCE﹣∠ACE=∠ACB﹣∠ACE,
即∠DCA=∠ECB,
∴△ACD≌△BCE(ASA),
∴CA=CB,
∴∠ABC=∠BAC=![]() ;
;
(2)如图③,过点C作CD⊥OM于点D,CE⊥ON于点E,

由(1)知:△ACD≌△BCE(ASA),△OCD≌△OCE(HL),
∴AD=BE,OD=OE
∵OD+OE=OA﹣AD+OB+BE=OA+OB=6+4=10,
∴OD=OE=5,
∵OC平分∠MON,
∴∠AOC=![]() ∠MON=30°,
∠MON=30°,
∵![]() =cos∠AOC,
=cos∠AOC,
∴OC=![]() .
.


 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为边在
为边在![]() 的另一侧作
的另一侧作![]() ,点
,点![]() 为射线
为射线![]() 上任意一点,在射线
上任意一点,在射线![]() 上截取
上截取![]() ,连接
,连接![]() 、
、![]() 、
、![]() .
.
(1)如图1,当点![]() 落在线段
落在线段![]() 的延长线上时,求
的延长线上时,求![]() 的度数;
的度数;
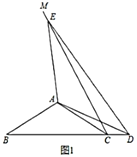
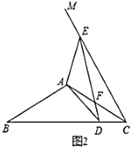
(2)如图2,当点![]() 落在线段
落在线段![]() (不含边界)上时,
(不含边界)上时,![]() 与
与![]() 交于点
交于点![]() ,请问(1)中的结论是否仍成立?如果成立,请给出证明;如果不成立,请说明理由;
,请问(1)中的结论是否仍成立?如果成立,请给出证明;如果不成立,请说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第二届“一带一路”国际合作高峰论坛将于2019年4月在北京举行.为了让恩施特产走出大山,走向世界,恩施一民营企业计划生产甲、乙两种商品共10万件,销住“一带一路”沿线国家和地区.已知3件甲种商品与2件乙种商品的销售收入相同,1件甲种商品比2件乙种商品的销售收入少600元.甲、乙两种商品的销售利润分别为120元和200元
(1)甲、乙两种商品的销售单价各多少元?
(2)市场调研表明:所有商品能全部售出,企业要求生产乙种商品的数量不超过甲种商品数量的![]() ,且甲、乙两种商品的销售总收入不低于3300万元,请你为该企业设计一种生产方案,使销售总利润最大.
,且甲、乙两种商品的销售总收入不低于3300万元,请你为该企业设计一种生产方案,使销售总利润最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
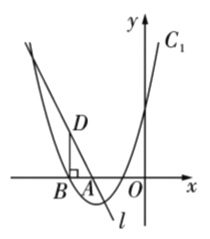
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 与
与![]() 轴的一个交点为
轴的一个交点为![]() (点
(点![]() 在点
在点![]() 的左侧),过点
的左侧),过点![]() 作
作![]() 垂直
垂直![]() 轴交直线
轴交直线![]() 于点
于点![]() .
.
(1)求抛物线的函数表达式;
(2)将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,点
,点![]() 的对应点分别为点
的对应点分别为点![]()
①求点![]() 的坐标;
的坐标;
②将拋物线![]() 向右平移使它经过点
向右平移使它经过点![]() ,此时得到的抛物线记为
,此时得到的抛物线记为![]() ,求出抛物线
,求出抛物线![]() 的函数表达式.
的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为 ;
(2)将条形统计图补充完整.观察此图,支付方式的“众数”是“ ”;
(3)在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲口袋中装有2个相同的小球,它们分别写有数值![]() ;乙口袋中装有3个相同的小球,它们分别写有数值
;乙口袋中装有3个相同的小球,它们分别写有数值![]() .现从甲口袋中随机取一球,记它上面的数值为
.现从甲口袋中随机取一球,记它上面的数值为![]() ,再从乙口袋中随机取一球,记它上面的数值为
,再从乙口袋中随机取一球,记它上面的数值为![]() .设点
.设点![]() 的坐标为
的坐标为![]() .
.
(1)请用树状图或列表法,列出![]() 所有可能的结果;
所有可能的结果;
(2)求点![]() 落在第一象限的概率.
落在第一象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科幻小说《实验室的故事》中,有这样一个情节,科学家把一种珍奇的植物分别放在不同温度的环境中,经过一天后,测试出这种植物高度的增长情况(如表):
温度 | …… |
|
| 0 | 2 | 4 | 4.5 | …… |
植物每天高度增长量 | …… | 41 | 49 | 49 | 41 | 25 | 19.75 | …… |
由这些数据,科学家推测出植物每天高度增长量![]() 是温度
是温度![]() 的函数,且这种函数是一次函数和二次函数中的一种.
的函数,且这种函数是一次函数和二次函数中的一种.
(1)请你选择一种适当的函数,求出它的函数关系式,并简要说明不选择另外一种函数的理由;
(2)如果实验室温度保持不变,在10天内要使该植物高度增长量的总和超过![]() ,那么实验室的温度
,那么实验室的温度![]() 应该在哪个范围内选择?请说明理由.
应该在哪个范围内选择?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016广西贺州市)如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(﹣2,5)的对应点A′的坐标是( )
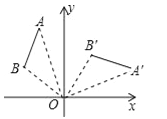
A. (2,5) B. (5,2) C. (2,﹣5) D. (5,﹣2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com