
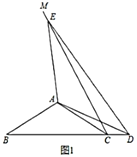
【题目】在![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为边在
为边在![]() 的另一侧作
的另一侧作![]() ,点
,点![]() 为射线
为射线![]() 上任意一点,在射线
上任意一点,在射线![]() 上截取
上截取![]() ,连接
,连接![]() 、
、![]() 、
、![]() .
.
(1)如图1,当点![]() 落在线段
落在线段![]() 的延长线上时,求
的延长线上时,求![]() 的度数;
的度数;
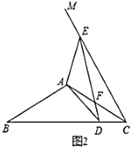
(2)如图2,当点![]() 落在线段
落在线段![]() (不含边界)上时,
(不含边界)上时,![]() 与
与![]() 交于点
交于点![]() ,请问(1)中的结论是否仍成立?如果成立,请给出证明;如果不成立,请说明理由;
,请问(1)中的结论是否仍成立?如果成立,请给出证明;如果不成立,请说明理由;
科目:初中数学 来源: 题型:
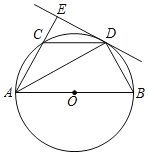
【题目】如图,AB是⊙O的直径,C点在⊙O上,AD平分角∠BAC交⊙O于D,过D作直线AC的垂线,交AC的延长线于E,连接BD,CD.
(1)求证:BD=CD;
(2)求证:直线DE是⊙O的切线;
(3)若DE=![]() ,AB=4,求AD的长.
,AB=4,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=3,点M在CD的边上,且DM=1,ΔAEM与ΔADM关于AM所在的直线对称,将ΔADM按顺时针方向绕点A旋转90°得到ΔABF,连接EF,则线段EF的长为( )
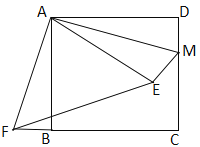
A. 3 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
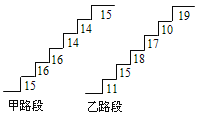
【题目】在某旅游景区上山的一条小路上,有一些断断续续的台阶,下图是其中的甲、乙两段台阶的示意图,图中的数字表示每一级台阶的高度(单位:cm).请你用所学过的有关统计知识,回答下列问题(数据:15,16,16,14,14,15的方差![]() ,数据:11,15,18,17,10,19的方差
,数据:11,15,18,17,10,19的方差![]() :
:
(1)分别求甲、乙两段台阶的高度平均数;
(2)哪段台阶走起来更舒服?与哪个数据(平均数、中位数、方差和极差)有关?
(3)为方便游客行走,需要陈欣整修上山的小路,对于这两段台阶路.在总高度及台阶数不变的情况下,请你提出合理的整修建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了创建国家级卫生城区,某社区在九月份购买了甲、乙两种绿色植物共1100盆,共花费了27000元.已知甲种绿色植物每盆20元,乙种绿色植物每盆30元.
(1)该社区九月份购买甲、乙两种绿色植物各多少盆?
(2)十月份,该社区决定再次购买甲、两种绿色植物.已知十月份甲种绿色植物每盆的价格比九月份的价格优惠![]() 元
元![]() ,十月份乙种绿色植物每盆的价格比九月份的价格优惠
,十月份乙种绿色植物每盆的价格比九月份的价格优惠![]() .因创卫需要,该社区十月份购买甲种绿色植物的数量比九月份的数量增加了
.因创卫需要,该社区十月份购买甲种绿色植物的数量比九月份的数量增加了![]() ,十为份购买乙种绿色植物的数量比九月份的数量增加了
,十为份购买乙种绿色植物的数量比九月份的数量增加了![]() .若该社区十月份的总花费与九月份的总花费恰好相同,求
.若该社区十月份的总花费与九月份的总花费恰好相同,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(感知)“如图①,![]() ,
,![]() 平分
平分![]() ,作
,作![]() ,
,![]() 、
、![]() 分别交射线
分别交射线![]() 、
、![]() 于
于![]() 、
、![]() 两点,连结
两点,连结![]() ,求
,求![]() 的度数”为了求解问题,某同学做了如下的分析,
的度数”为了求解问题,某同学做了如下的分析,
“过点![]() 作
作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,”进而求解,则
,”进而求解,则![]() ________
________![]() .
.
(拓展)如图②,一般地,设![]()
![]() ,
,![]() 平分
平分![]() ,作
,作![]() ,
,![]() 、
、![]() 分别交射线
分别交射线![]() 、
、![]() 于
于![]() 、
、![]() 两点,连结
两点,连结![]() .
.
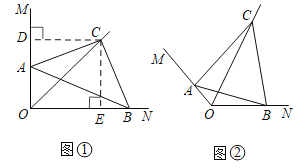
(1)求![]() 的度数.(用含
的度数.(用含![]() 的代数式表示)
的代数式表示)
(2)若![]() ,
,![]() ,
,![]() ,则
,则![]() ________.
________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,抛物线的对称轴与
,抛物线的对称轴与![]() 轴交于点
轴交于点![]() ,顶点坐标为
,顶点坐标为![]() .
.
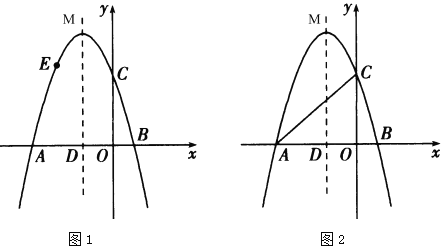
(1)求抛物线的表达式和顶点![]() 的坐标;
的坐标;
(2)如图1,点![]() 为抛物线上一点,点
为抛物线上一点,点![]() 不与点
不与点![]() 重合,当
重合,当![]() 时,过点
时,过点![]() 作
作![]() 轴,交抛物线的对称轴于点
轴,交抛物线的对称轴于点![]() ,作
,作![]() 轴于点H,得到矩形
轴于点H,得到矩形![]() ,求矩形
,求矩形![]() 的周长的最大值;
的周长的最大值;
(3)如图2,点![]() 为抛物线对称轴上一点,是否存在点
为抛物线对称轴上一点,是否存在点![]() ,使以点
,使以点![]() 、
、![]() 、
、![]() 为顶点的三角形是直角三角形?若存在,求出点
为顶点的三角形是直角三角形?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com