
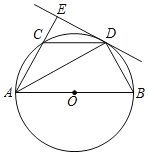
【题目】如图,AB是⊙O的直径,C点在⊙O上,AD平分角∠BAC交⊙O于D,过D作直线AC的垂线,交AC的延长线于E,连接BD,CD.
(1)求证:BD=CD;
(2)求证:直线DE是⊙O的切线;
(3)若DE=![]() ,AB=4,求AD的长.
,AB=4,求AD的长.
【答案】(1)证明见解析;(2)证明见解析;(3)AD=2![]() .
.
【解析】
(1)由角平分线定义得出∠CAD=∠BAD,即可得出结论;
(2)连接半径OD,则OD=OA,得出∠OAD=∠ODA,由∠EAD+∠ADE=90°,∠EAD=∠BAD,得出∠BAD+∠ADE=90°,即∠ODA+∠ADE=90°,即可得出结论;
(3)过点D作DF⊥AB于F,则DF=DE=![]() ,由勾股定理得出OF=
,由勾股定理得出OF=![]() =1,易证△OBD是等边三角形,得出OF=FB=1,AF=AB-FB=3,由勾股定理即可得出结果.
=1,易证△OBD是等边三角形,得出OF=FB=1,AF=AB-FB=3,由勾股定理即可得出结果.
(1)证明:∵在⊙O中,AD平分角∠BAC,
∴∠CAD=∠BAD,
∴BD=CD;
(2)证明:连接半径OD,如图1所示:
则OD=OA,
∴∠OAD=∠ODA,
∵DE⊥AC于E,在Rt△ADE中,
∴∠EAD+∠ADE=90°,
由(1)知∠EAD=∠BAD,
∴∠BAD+∠ADE=90°,即∠ODA+∠ADE=90°,
∴OD⊥DE,
∴DE是⊙O的切线;
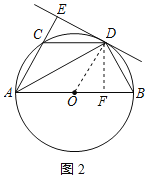
(3)解:过点D作DF⊥AB于F,如图2所示:
则DF=DE=![]() ,
,
∵AB=4,
∴半径OD=2,
在Rt△ODF中,OF=![]() =
=![]() =1,
=1,
∴∠ODF=30°,
∴∠DOB=60°,
∵OD=OB,
∴△OBD是等边三角形,
∴OF=FB=1,
∴AF=AB﹣FB=4﹣1=3,
在Rt△ADF中,AD=![]() =
=![]() =2
=2![]() .
.


科目:初中数学 来源: 题型:
【题目】下面是“经过已知直线外一点作这条直线的平行线”的尺规作图过程.
己知:如图1,直线![]() 和直线
和直线![]() 外一点
外一点![]() .
.
求作:直线![]() 的平行直线,使它经过点
的平行直线,使它经过点![]() .
.

作法:如图2,
(1)过![]() 作直线
作直线![]() 与直线
与直线![]() 交于点
交于点![]() ;
;
(2)在直线![]() 取一点
取一点![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 长为半径画弧,与直线
长为半径画弧,与直线![]() 交于点
交于点![]() ;
;
(3)以点![]() 为圆心,
为圆心,![]() 长为半径画弧,交直线
长为半径画弧,交直线![]() 于点
于点![]() 以点
以点![]() 为圆心,
为圆心,![]() 长为半径画弧,两弧交于点
长为半径画弧,两弧交于点![]() ;
;
(4)作直线![]() .
.
所以,直线![]() 就是所求作的平行线.
就是所求作的平行线.
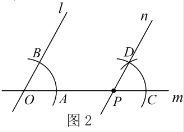
请回答:该作图的依据是______________________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,点E是CD上一点(不与C,D两点重合),连接BE,过点C作CH⊥BE于点F,交对角线BD于点G,交AD边于点H,连接GE,
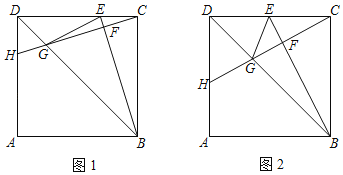
(1)求证:△DHC≌△CEB;
(2)如图2,若点E是CD的中点,当BE=8时,求线段GH的长;
(3)设正方形ABCD的面积为S1,四边形DEGH的面积为S2,当![]() 的值为
的值为![]() 时,
时,![]() 的值为 .
的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋中装有相同的三个小球,其上面分别标注数字1、2、3、,现从中任意摸出一个小球,将其上面的数字作为点M的横坐标;将球放回袋中搅匀,再从中任意摸出一个小球,将其上面的数字作为点M的纵坐标.
(1)求点M在直线y=x上的概率;
(2)求点M的横坐标与纵坐标之和是偶数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
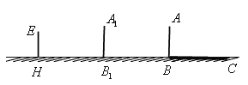
【题目】学习投影后,小明、小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时间,身高为![]() 的小明
的小明![]() 的影子
的影子![]() 长是
长是![]() ,而小颖
,而小颖![]() 刚好在路灯灯泡的正下方
刚好在路灯灯泡的正下方![]() 点,并测得
点,并测得![]() .
.
(1)请在图中画出形成影子的光线,并确定路灯灯泡所在的位置![]() ;
;
(2)求路灯灯泡的垂直高度![]() ;
;
(3)如果小明沿线段BH向小颖(点H)走去,当小明走到BH中点B1处时,请在图中画出此时小明的影长B1C1,并求B1C1的长;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 是
是![]() 的直径,且
的直径,且![]() ,
,![]() 是
是![]() 上一点,将弧
上一点,将弧![]() 沿直线
沿直线![]() 翻折,使翻折后的圆弧恰好经过圆心
翻折,使翻折后的圆弧恰好经过圆心![]() ,则
,则
(1)![]() 的长是_________.
的长是_________.
(2)劣弧![]() 的长是__________.
的长是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
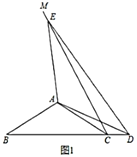
【题目】在![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为边在
为边在![]() 的另一侧作
的另一侧作![]() ,点
,点![]() 为射线
为射线![]() 上任意一点,在射线
上任意一点,在射线![]() 上截取
上截取![]() ,连接
,连接![]() 、
、![]() 、
、![]() .
.
(1)如图1,当点![]() 落在线段
落在线段![]() 的延长线上时,求
的延长线上时,求![]() 的度数;
的度数;
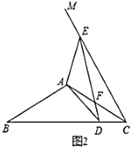
(2)如图2,当点![]() 落在线段
落在线段![]() (不含边界)上时,
(不含边界)上时,![]() 与
与![]() 交于点
交于点![]() ,请问(1)中的结论是否仍成立?如果成立,请给出证明;如果不成立,请说明理由;
,请问(1)中的结论是否仍成立?如果成立,请给出证明;如果不成立,请说明理由;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com