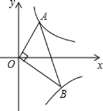
【题目】如图，已知点A、B分别在反比例函数
，
的图象上，且OA
OB， 则
的值为 ____________ ．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】4月23日是世界读书日，某校为了解学生课外阅读情况，抽样调查了部分学生每周用于课外阅读的时间，过程如下：
数据收集：从全校随机抽取20名学生，进行了每周用于课外阅读时间的调查，数据如下(单位：
)
30 | 60 | 81 | 50 | 40 | 110 | 130 | 146 | 90 | 100 |
60 | 81 | 120 | 140 | 70 | 81 | 10 | 20 | 100 | 81 |
整理数据：按如下分段整理样本数据并补全表格：
课外阅读时间 |
|
|
|
|
等级 |
|
|
|
|
人数 | 3 |
| 8 |
|
分析数据：补全下列表格中的统计量：
平均数 | 中位数 | 众数 |
80 |
|
|
（1）
，
，
，
；
（2）用样本中的统计量估计该校学生每周用于课外阅读时间的情况等级为 ；
（3）如果该校现有学生400人，估计等级为“
”的学生有多少名？
查看答案和解析>>
科目：初中数学 来源： 题型：
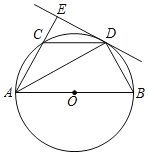
【题目】如图，AB是⊙O的直径，C点在⊙O上，AD平分角∠BAC交⊙O于D，过D作直线AC的垂线，交AC的延长线于E，连接BD，CD．
（1）求证：BD＝CD；
（2）求证：直线DE是⊙O的切线；
（3）若DE＝
，AB＝4，求AD的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在菱形
中，对角线
与
交于点
，
，
，点
是对角线上一点（可与
，
重合），以点为圆心，
为半径作
（其中
）．
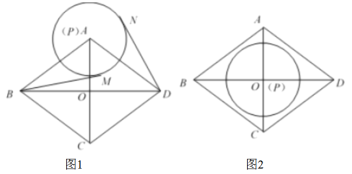
（1）如图1，当点与重合，且
时，过点
，
分别作的切线，切点分别为
，
．求证：
；
（2）如图2，当点与点重合，且在菱形内部时（不含边界），求的取值范围；
（3）当点为
或
的内心时，直接写出
的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】开学初期，天气炎热，水杯需求量大．双福育才中学门口某超市购进一批水杯，其中A种水杯进价为每个15元，售价为每个25元；B种水杯进价为每个12元，售价为每个20元
（1）该超市平均每天可售出60个A种水杯，后来经过市场调查发现，A种水杯单价每降低1元，则平均每天的销量可增加10个．为了尽量让学生得到更多的优惠，某天该超市将A种水杯售价调整为每个m元，结果当天销售A种水杯获利630元，求m的值．
（2）该超市准备花费不超过1600元的资金，购进A、B两种水杯共120个，其中B种水杯的数量不多于A种水杯数量的两倍．请为该超市设计获利最大的进货方案，并求出最大利润．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知直线y=kx+b交x轴于点A(1，0) ，与双曲线
交于点
（1）求直线AB的解析式为____ ____________；
（2）若 x 轴上存在动点 M（m，0），过点 M 且与 x 轴垂直的直线与直线AB交于点C，与双曲线交于点D(C、D两点不重合），当BC >BD时，写出m的取值范围_____________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（感知）“如图①，
，
平分
，作
，
、
分别交射线
、
于
、
两点，连结
，求
的度数”为了求解问题，某同学做了如下的分析，
“过点
作
于点
，
于点
，”进而求解，则
________
．
（拓展）如图②，一般地，设
，平分，作
，、分别交射线、于、两点，连结．
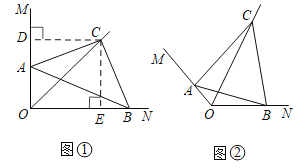
（1）求的度数．（用含
的代数式表示）
（2）若
，
，
，则
________．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
