
【题目】在菱形![]() 中,对角线
中,对角线![]() 与
与![]() 交于点
交于点![]() ,
,![]() ,
,![]() ,点
,点![]() 是对角线
是对角线![]() 上一点(可与
上一点(可与![]() ,
,![]() 重合),以点
重合),以点![]() 为圆心,
为圆心,![]() 为半径作
为半径作![]() (其中
(其中![]() ).
).
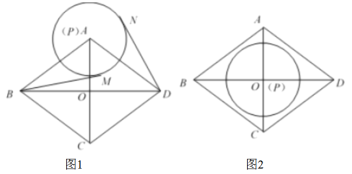
(1)如图1,当点![]() 与
与![]() 重合,且
重合,且![]() 时,过点
时,过点![]() ,
,![]() 分别作
分别作![]() 的切线,切点分别为
的切线,切点分别为![]() ,
,![]() .求证:
.求证:![]() ;
;
(2)如图2,当点![]() 与点
与点![]() 重合,且
重合,且![]() 在菱形
在菱形![]() 内部时(不含边界),求
内部时(不含边界),求![]() 的取值范围;
的取值范围;
(3)当点![]() 为
为![]() 或
或![]() 的内心时,直接写出
的内心时,直接写出![]() 的长.
的长.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)连接![]() ,
,![]() ,则AM=AN,根据切线的性质可得
,则AM=AN,根据切线的性质可得![]() 90°,据此通过“HL”证明Rt△BMA与Rt△DNA全等,最后利用全等三角形性质证明结论即可;
90°,据此通过“HL”证明Rt△BMA与Rt△DNA全等,最后利用全等三角形性质证明结论即可;
(2)当点![]() 与点
与点![]() 重合,
重合,![]() 在菱形内部时,过点P作
在菱形内部时,过点P作![]() 于点
于点![]() ,根据菱形的性质可得
,根据菱形的性质可得![]() ,
,![]() ,由此进一步利用勾股定理计算出
,由此进一步利用勾股定理计算出![]() ,最后通过
,最后通过![]() 结合题意进一步分析求解即可;
结合题意进一步分析求解即可;
(3)如图,当点![]() 为
为![]() 内心时,过
内心时,过![]() 作
作![]() 于
于![]() ,作
,作![]() 于
于![]() ,则有
,则有![]() ,连接
,连接![]() 、
、![]() ,根据
,根据![]() 求出此时圆的半径,从而根据
求出此时圆的半径,从而根据![]() 直接计算即可,然后当点
直接计算即可,然后当点![]() 为
为![]() 的内心时,按照相同的方法进一步求解即可.
的内心时,按照相同的方法进一步求解即可.
(1)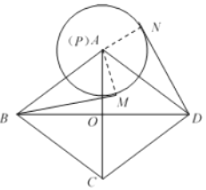
如图,连接![]() ,
,![]() ,则AM=AN,
,则AM=AN,
∵![]() ,
,![]() 分别是
分别是![]() 的切线,
的切线,
∴![]() 90°,
90°,
∵四边形ABCD是菱形,
∴AB=AD,
∴在Rt△BMA与Rt△DNA中,
∵![]() ,
,![]() ,
,
∴![]()
![]() ,
,
∴![]() ;
;
(2)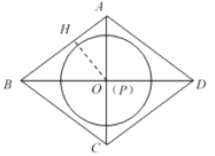
如图,当点![]() 与点
与点![]() 重合,
重合,![]() 在菱形内部时,过点P作
在菱形内部时,过点P作![]() 于点
于点![]() ,
,
![]() 在菱形
在菱形![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
由![]() ,得
,得![]() ,
,
解得:![]() ,
,
∴当点![]() 与点
与点![]() 重合,且
重合,且![]() 在菱形
在菱形![]() 内部时,
内部时,![]() 的取值范围是:
的取值范围是:![]() ;
;
(3)AP长为![]() 或
或![]() .
.
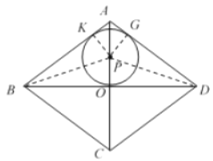
如图,当点![]() 为
为![]() 内心时,过
内心时,过![]() 作
作![]() 于
于![]() ,作
,作![]() 于
于![]() ,
,
则有![]() ,连接
,连接![]() 、
、![]() ,
,
则有![]() ,
,
由菱形性质可得:AB=AD=BC=CD=5,AO=OC=3,BO=OD=4,
∴![]() ,
,
解得:![]() ,
,
则![]() ;
;
当点![]() 为
为![]() 的内心时,同理可得
的内心时,同理可得![]() ,
,
综上所诉,![]() 或
或![]() .
.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,连接AD,E为AD的中点,过A作AF∥BC交BE延长线于F,连接CF.
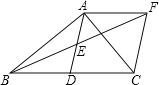
(1)求证:四边形ADCF是菱形;
(2)在不添加任何辅助线的情况下,请直接写出与△ACD面积相等的三角形(不包含△ACD).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋中装有相同的三个小球,其上面分别标注数字1、2、3、,现从中任意摸出一个小球,将其上面的数字作为点M的横坐标;将球放回袋中搅匀,再从中任意摸出一个小球,将其上面的数字作为点M的纵坐标.
(1)求点M在直线y=x上的概率;
(2)求点M的横坐标与纵坐标之和是偶数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
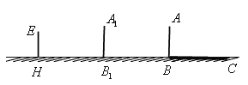
【题目】学习投影后,小明、小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时间,身高为![]() 的小明
的小明![]() 的影子
的影子![]() 长是
长是![]() ,而小颖
,而小颖![]() 刚好在路灯灯泡的正下方
刚好在路灯灯泡的正下方![]() 点,并测得
点,并测得![]() .
.
(1)请在图中画出形成影子的光线,并确定路灯灯泡所在的位置![]() ;
;
(2)求路灯灯泡的垂直高度![]() ;
;
(3)如果小明沿线段BH向小颖(点H)走去,当小明走到BH中点B1处时,请在图中画出此时小明的影长B1C1,并求B1C1的长;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 是
是![]() 的直径,且
的直径,且![]() ,
,![]() 是
是![]() 上一点,将弧
上一点,将弧![]() 沿直线
沿直线![]() 翻折,使翻折后的圆弧恰好经过圆心
翻折,使翻折后的圆弧恰好经过圆心![]() ,则
,则
(1)![]() 的长是_________.
的长是_________.
(2)劣弧![]() 的长是__________.
的长是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
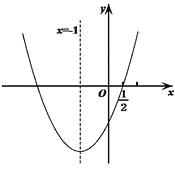
【题目】如图,二次函数![]() 的图象经过点
的图象经过点![]() ,对称轴为直线
,对称轴为直线![]() ,下列5个结论:①
,下列5个结论:①![]() ; ②
; ②![]() ; ③
; ③![]() ;④
;④![]() ; ⑤
; ⑤![]() ,其中正确的结论为________________.(注:只填写正确结论的序号)
,其中正确的结论为________________.(注:只填写正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
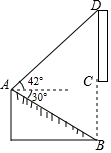
【题目】小婷在放学路上,看到隧道上方有一块宣传“中国﹣南亚博览会”的竖直标语牌CD.她在A点测得标语牌顶端D处的仰角为42°,测得隧道底端B处的俯角为30°(B,C,D在同一条直线上),AB=10m,隧道高6.5m(即BC=65m),求标语牌CD的长(结果保留小数点后一位).(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第二届“一带一路”国际合作高峰论坛将于2019年4月在北京举行.为了让恩施特产走出大山,走向世界,恩施一民营企业计划生产甲、乙两种商品共10万件,销住“一带一路”沿线国家和地区.已知3件甲种商品与2件乙种商品的销售收入相同,1件甲种商品比2件乙种商品的销售收入少600元.甲、乙两种商品的销售利润分别为120元和200元
(1)甲、乙两种商品的销售单价各多少元?
(2)市场调研表明:所有商品能全部售出,企业要求生产乙种商品的数量不超过甲种商品数量的![]() ,且甲、乙两种商品的销售总收入不低于3300万元,请你为该企业设计一种生产方案,使销售总利润最大.
,且甲、乙两种商品的销售总收入不低于3300万元,请你为该企业设计一种生产方案,使销售总利润最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com