
【题目】如图,正方形![]() 的对角线
的对角线![]() 、
、![]() 相交于点
相交于点![]() ,
,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .若
.若![]() ,则
,则![]() ____.
____.
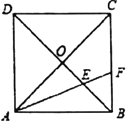
【答案】4
【解析】
作EG⊥AB,得△EBG是等腰直角三角形,再利用角平分线的性质可得△EGB是等腰直角三角形,即可求出BE的长,进而可求出OB、BC的长,根据直角三角形两锐角互余的关系可得∠EFB=∠FEB,即可证明BE=BF,根据CF=BC-BF即可得答案.
作EG⊥AB于G,
∵AF是∠CAB的角平分线,OE⊥AC,
∴EG=OE=2,
∵ABCD是正方形,BD是对角线,
∴∠ABE=45°
∴△EBG是等腰直角三角形,
可得BE=![]() EG=2
EG=2![]() ,
,
∴OB=2+2![]()
∴BC=2![]() OB=4+2
OB=4+2![]()
∵∠AFB=90°-∠FAB,∠FEB=∠OEA=90°-∠FAC,∠FAC=∠FAB,
∴∠AFB=∠FEB
∴BF=BE=2![]()
∴CF=BC-BF=4+2![]() -2
-2![]() =4.
=4.
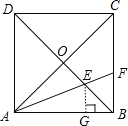
故答案为:4


 高效智能课时作业系列答案
高效智能课时作业系列答案科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,点E是CD上一点(不与C,D两点重合),连接BE,过点C作CH⊥BE于点F,交对角线BD于点G,交AD边于点H,连接GE,
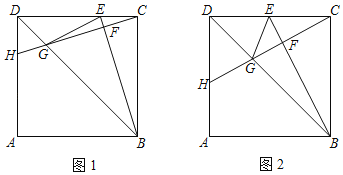
(1)求证:△DHC≌△CEB;
(2)如图2,若点E是CD的中点,当BE=8时,求线段GH的长;
(3)设正方形ABCD的面积为S1,四边形DEGH的面积为S2,当![]() 的值为
的值为![]() 时,
时,![]() 的值为 .
的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 是
是![]() 的直径,且
的直径,且![]() ,
,![]() 是
是![]() 上一点,将弧
上一点,将弧![]() 沿直线
沿直线![]() 翻折,使翻折后的圆弧恰好经过圆心
翻折,使翻折后的圆弧恰好经过圆心![]() ,则
,则
(1)![]() 的长是_________.
的长是_________.
(2)劣弧![]() 的长是__________.
的长是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系 xOy 中,已知抛物线y= x2 -2px+q.
(1)当p=2 时,
①抛物线的顶点坐标横坐标为____ ___,纵坐标为__________(用含 q 的式子表示);
②若点 A(-1,y1),B(x2,y2 )都在抛物线上,且y2 >y1,令x2 = m,则 m的取值范围是_____________;
(2)已知点 M(3,2),将点 M 向左平移 5 个单位长度,得到点 N.当q=6 时,若抛物线与线段 MN 恰有一个公共点,结合函数图象,求 p 的取值范围为_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
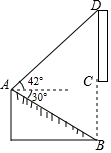
【题目】小婷在放学路上,看到隧道上方有一块宣传“中国﹣南亚博览会”的竖直标语牌CD.她在A点测得标语牌顶端D处的仰角为42°,测得隧道底端B处的俯角为30°(B,C,D在同一条直线上),AB=10m,隧道高6.5m(即BC=65m),求标语牌CD的长(结果保留小数点后一位).(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为边在
为边在![]() 的另一侧作
的另一侧作![]() ,点
,点![]() 为射线
为射线![]() 上任意一点,在射线
上任意一点,在射线![]() 上截取
上截取![]() ,连接
,连接![]() 、
、![]() 、
、![]() .
.
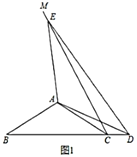
(1)如图1,当点![]() 落在线段
落在线段![]() 的延长线上时,求
的延长线上时,求![]() 的度数;
的度数;
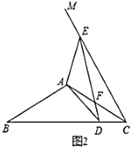
(2)如图2,当点![]() 落在线段
落在线段![]() (不含边界)上时,
(不含边界)上时,![]() 与
与![]() 交于点
交于点![]() ,请问(1)中的结论是否仍成立?如果成立,请给出证明;如果不成立,请说明理由;
,请问(1)中的结论是否仍成立?如果成立,请给出证明;如果不成立,请说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲口袋中装有2个相同的小球,它们分别写有数值![]() ;乙口袋中装有3个相同的小球,它们分别写有数值
;乙口袋中装有3个相同的小球,它们分别写有数值![]() .现从甲口袋中随机取一球,记它上面的数值为
.现从甲口袋中随机取一球,记它上面的数值为![]() ,再从乙口袋中随机取一球,记它上面的数值为
,再从乙口袋中随机取一球,记它上面的数值为![]() .设点
.设点![]() 的坐标为
的坐标为![]() .
.
(1)请用树状图或列表法,列出![]() 所有可能的结果;
所有可能的结果;
(2)求点![]() 落在第一象限的概率.
落在第一象限的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com