
【题目】在平面直角坐标系 xOy 中,已知抛物线y= x2 -2px+q.
(1)当p=2 时,
①抛物线的顶点坐标横坐标为____ ___,纵坐标为__________(用含 q 的式子表示);
②若点 A(-1,y1),B(x2,y2 )都在抛物线上,且y2 >y1,令x2 = m,则 m的取值范围是_____________;
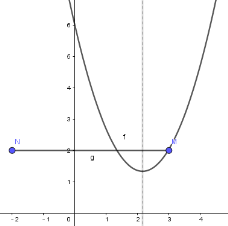
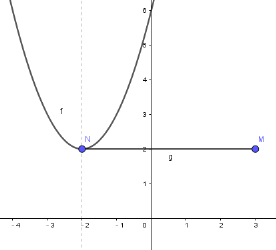
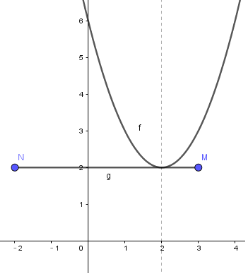
(2)已知点 M(3,2),将点 M 向左平移 5 个单位长度,得到点 N.当q=6 时,若抛物线与线段 MN 恰有一个公共点,结合函数图象,求 p 的取值范围为_____________.
【答案】(1)①2,q- 4;②m![]() 1或m
1或m ![]() 5;(2)p≤-2 或p=2或
5;(2)p≤-2 或p=2或![]() .
.
【解析】
(1)①将P的值代入,将函数解析式改写为顶点式,即可求解. ②由对称轴为x=2,可得x=-1与x=5的函数值相等,数形结合可知当y2 >y1时,x2的取值范围,即m的范围为x2 ![]() 1或x2
1或x2 ![]() 5
5
(2)由于线段MN//x轴,满足线段MN与抛物线只有一个交点,通过数形结合,分线段MN的左,右端点在抛物线上和抛物线的顶点在线段上三种情况,分别得到关于P的方程求解即可.
(1)①∵ p=2 ,
∴抛物线为y=x2 - 4x+q= (x- 2)2 +q- 4 .
∴顶点的坐标为( 2,q- 4).
②

由对称轴为x=2,由图可知,当x=-1与x=5的函数值相等,点A(-1,y1), B(x2,y2 ), 要使y2 >y1,则点B应在点A的左上方或在点![]() 的右上方,故有x2
的右上方,故有x2![]() 1或 x2
1或 x2![]() 5;而x2 = m,所以m的取值范围为m
5;而x2 = m,所以m的取值范围为m![]() 1或m
1或m ![]() 5.
5.
(2)∵点M(3,2)向左平移 5 个单位得到点N,
∴点N的坐标为(-2 ,2).
∵q= 6 ,
∴抛物线为y=x2 -2px+ 6 .
当抛物线经过点M(3,2)时, 2 = 32 - 6p+ 6 ,解得p![]() .
.
当抛物线经过点N(-2 ,2)时, 2 = (-2)2 + 4 p+ 6 ,解得 p=-2 .
当抛物线的顶点在线段PQ上时,6 - p2 = 2 ,解得p=±2 .
满足线段MN与抛物线只有一个交点,结合图象可知,m的取值范围是p≤-2 或p=2或![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在“阳光体育”活动时间,小英、小丽、小敏、小洁四位同学进行一次羽毛球单打比赛,要从中选出两位同学打第一场比赛.
(1)若已确定小英打第一场,再从其余三位同学中随机选取一位,求恰好选中小丽同学的概率;
(2)用画树状图或列表的方法,求恰好选中小敏、小洁两位同学进行比赛的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着交通道路的不断完善,带动了旅游业的发展,某市旅游景区有A、B、C、D、E等著名景点,该市旅游部门统计绘制出2017年“五一”长假期间旅游情况统计图,根据以下信息解答下列问题:

(1)2017年“五一”期间,该市周边景点共接待游客 万人,扇形统计图中A景点所对应的圆心角的度数是 ,并补全条形统计图.
(2)根据近几年到该市旅游人数增长趋势,预计2018年“五一”节将有80万游客选择该市旅游,请估计有多少万人会选择去E景点旅游?
(3)甲、乙两个旅行团在A、B、D三个景点中,同时选择去同一景点的概率是多少?请用画树状图或列表法加以说明,并列举所用等可能的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】开学初期,天气炎热,水杯需求量大.双福育才中学门口某超市购进一批水杯,其中A种水杯进价为每个15元,售价为每个25元;B种水杯进价为每个12元,售价为每个20元
(1)该超市平均每天可售出60个A种水杯,后来经过市场调查发现,A种水杯单价每降低1元,则平均每天的销量可增加10个.为了尽量让学生得到更多的优惠,某天该超市将A种水杯售价调整为每个m元,结果当天销售A种水杯获利630元,求m的值.
(2)该超市准备花费不超过1600元的资金,购进A、B两种水杯共120个,其中B种水杯的数量不多于A种水杯数量的两倍.请为该超市设计获利最大的进货方案,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形 ABCD 中,M,N,P,Q 分别为边 AB,BC,CD,DA 上的点(不与端点重合).对于任意矩形 ABCD,下面四个结论中:①存在无数个四边形 MNPQ 是平行四边形;②存在无数个四边形 MNPQ 是矩形;③存在无数个四边形 MNPQ 是菱形;④不存在四边形 MNPQ 是正方形.所有正确结论的序号是_________________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形![]() 中,
中,![]() ,
,![]() ,以点
,以点![]() 为坐标原点,
为坐标原点,![]() 所在的直线为
所在的直线为![]() 轴,建立直角坐标系.
轴,建立直角坐标系.

(Ⅰ)将矩形![]() 绕点
绕点![]() 逆时针旋转至矩形
逆时针旋转至矩形![]() ,如图1,
,如图1,![]() 经过点
经过点![]() ,求旋转角的大小和点
,求旋转角的大小和点![]() ,
,![]() 的坐标;
的坐标;
(Ⅱ)将图1中矩形![]() 沿直线
沿直线![]() 向左平移,如图2,平移速度是每秒1个单位长度.
向左平移,如图2,平移速度是每秒1个单位长度.
①经过几秒,直线![]() 经过点
经过点![]() ;
;
②设两矩形重叠部分的面积为![]() ,运动时间为
,运动时间为![]() ,写出重叠部分面积
,写出重叠部分面积![]() 与时间
与时间![]() 之间的函数关系式.
之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
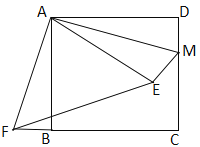
【题目】如图,在正方形ABCD中,AB=3,点M在CD的边上,且DM=1,ΔAEM与ΔADM关于AM所在的直线对称,将ΔADM按顺时针方向绕点A旋转90°得到ΔABF,连接EF,则线段EF的长为( )
A. 3 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
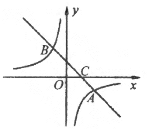
【题目】如图,在平面直角坐标系中,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像交于
的图像交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(1)求![]() 的值;
的值;
(2)请直接写出不等式![]() 的解集;
的解集;
(3)将![]() 轴下方的图像沿
轴下方的图像沿![]() 轴翻折,点
轴翻折,点![]() 落在点
落在点![]() 处,连接
处,连接![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com